

| Partial Differential Equations Toolbox |   |
u1=parabolic(u0,tlist,b,p,e,t,c,a,f,d) u1=parabolic(u0,tlist,b,p,e,t,c,a,f,d,rtol) u1=parabolic(u0,tlist,b,p,e,t,c,a,f,d,rtol,atol) u1=parabolic(u0,tlist,K,F,B,ud,M) u1=parabolic(u0,tlist,K,F,B,ud,M,rtol) u1=parabolic(u0,tlist,K,F,B,ud,M,rtol,atol)
Description
u1=parabolic(u0,tlist,g,b,p,e,t,c,a,f,d)
produces the solution to the FEM formulation of the scalar PDE problem
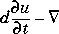 · (c
· (c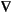 u) + au = f on
u) + au = f on 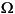 ,
,
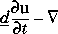 · (c
· (c 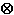
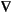 u) + au = f on
u) + au = f on 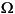 .
.
on a mesh described by p, e, and t, with boundary conditions given by b, and with initial value u0.
u1 is the solution at the coordinates given by the corresponding column in p. Each column in u1 is the solution at the time given by the corresponding item in tlist. For a system of dimension N with np node points, the first np rows of u1 describe the first component of u, the following np rows of u1 describe the second component of u, and so on. Thus, the components of u are placed in the vector u as N blocks of node point rows.
b
describes the boundary conditions of the PDE problem. b can be either a Boundary Condition matrix or the name of a Boundary M-file. The boundary conditions can depend on t, the time. The formats of the Boundary Condition matrix and Boundary M-file are described in the entries on assemb and pdebound, respectively.
The geometry of the PDE problem is given by the mesh data p, e, and t. Details on the mesh data representation can be found in the entry on initmesh.
The coefficients c, a, d, and f of the PDE problem can be given in a variety of ways. The coefficients can depend on t, the time. A complete listing of all options can be found in under the entry assempde.
atol and rtol are absolute and relative tolerances that are passed to the ODE solver.
u1=parabolic(u0,tlist,K,F,B,ud,M)
produces the solution to the ODE problem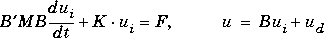
u0.
Examples
Solve the heat equation
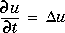
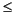 x,y
x,y 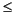 1 (
1 (squareg). Choose u(0) = 1 on the disk x2 +y2 < 0.42, and u(0) = 0 otherwise. Use Dirichlet boundary conditions u = 0 (squareb1). Compute the solution at times linspace(0,0.1,20).
» [p,e,t]=initmesh('squareg');
» [p,e,t]=refinemesh('squareg',p,e,t);
» u0=zeros(size(p,2),1);
» ix=find(sqrt(p(1,:).^2+p(2,:).^2)<0.4);
» u0(ix)=ones(size(ix));
» tlist=linspace(0,0.1,20);
» u1=parabolic(u0,tlist,'squareb1',p,e,t,1,0,1,1);
See Also
assempde, hyperbolic
 | jigglemesh | pdeadgsc |  |