Optimization Toolbox

Hessian Update

The direction of search is determined by a choice of either the BFGS (Eq. 2-6) or the DFP method given in Quasi-Newton Methods (set the options parameter HessUpdate to 'dfp' to select the DFP method). The Hessian, H, is always maintained to be positive definite so that the direction of search, d, is always in a descent direction. This means that for some arbitrarily small step, 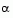, in the direction, d, the objective function decreases in magnitude. Positive definiteness of H is achieved by ensuring that H is initialized to be positive definite and thereafter 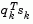(from Eq. 2-14) is always positive. The term 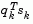is a product of the line search step length parameter, 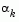and a combination of the search direction, d, with past and present gradient evaluations,

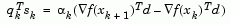
(2-14)

The condition that 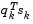is positive is always achieved by ensuring that a sufficiently accurate line search is performed. This is because the search direction, d, is a descent direction so that 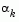and 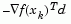are always positive. Thus, the possible negative term 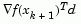can be made as small in magnitude as required by increasing the accuracy of the line search.

Quasi-Newton Implementation

Line Search Procedures