

| Optimization Toolbox |   |
Updating the Hessian Matrix
At each major iteration a positive definite quasi-Newton approximation of the Hessian of the Lagrangian function, H, is calculated using the BFGS method where 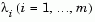 is an estimate of the Lagrange multipliers.
is an estimate of the Lagrange multipliers.
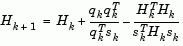 where where
|
(2-28) |
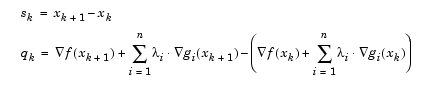
Powell [32] recommends keeping the Hessian positive definite even though it may be positive indefinite at the solution point. A positive definite Hessian is maintained providing 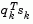 is positive at each update and that H is initialized with a positive definite matrix. When
is positive at each update and that H is initialized with a positive definite matrix. When 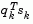 is not positive,
is not positive, 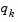 is modified on an element by element basis so that
is modified on an element by element basis so that 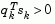 . The general aim of this modification is to distort the elements of
. The general aim of this modification is to distort the elements of 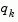 , which contribute to a positive definite update, as little as possible. Therefore, in the initial phase of the modification, the most negative element of
, which contribute to a positive definite update, as little as possible. Therefore, in the initial phase of the modification, the most negative element of 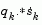 is repeatedly halved. This procedure is continued until
is repeatedly halved. This procedure is continued until 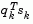 is greater than or equal to 1e-5. If after this procedure,
is greater than or equal to 1e-5. If after this procedure, 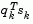 is still not positive,
is still not positive, 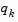 is modified by adding a vector v multiplied by a constant scalar w, that is,
is modified by adding a vector v multiplied by a constant scalar w, that is,
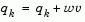
|
(2-29) |
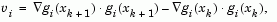
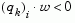 and
and 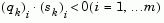
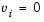 otherwise
otherwise
and w is systematically increased until 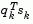 becomes positive.
becomes positive.
The functions fmincon, fminimax, fgoalattain, and fseminf all use SQP. If the options parameter Display is set to 'iter', then various information is given such as function values and the maximum constraint violation. When the Hessian has to be modified using the first phase of the procedure described above to keep it positive definite, then Hessian modified is displayed. If the Hessian has to be modified again using the second phase of the approach described above, then Hessian modified twice is displayed. When the QP subproblem is infeasible, then infeasible is displayed. Such displays are usually not a cause for concern but indicate that the problem is highly nonlinear and that convergence may take longer than usual. Sometimes the message no update is displayed indicating that 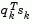 is nearly zero. This can be an indication that the problem setup is wrong or you are trying to minimize a noncontinuous function.
is nearly zero. This can be an indication that the problem setup is wrong or you are trying to minimize a noncontinuous function.
 | SQP Implementation | Quadratic Programming Solution |  |