tustin (Mu Analysis and Synthesis Toolbox)

Create a discrete-time version of a continuous-time SYSTEM matrix using a bilinear or prewarped tustin transformation

Syntax

dsys = tustin(csys,T,prewarpf)

Description
The packed continuous SYSTEM matrix, csys, is converted into a discrete-time SYSTEM matrix, dsys, using a bilinear transformation with prewarping. The argument T is the sample time, in seconds. prewarpf is the prewarp frequency in rads/sec. prewarpf is an optional argument, and if omitted, or equal to zero, a bilinear transformation is performed instead.

The resulting discrete system, dsys, has the same transfer function at the continuous system, csys, at the prewarp frequency. Choosing a prewarp frequency close to the crossover frequency is often appropriate for a control system. Choosing a prewarp frequency too close to the Nyquist frequency (1/2T) can result in severe distortion at the lower frequencies. In the extreme, if prewarp is greater than or equal to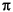

/T, the discrete system can be unstable.

Note that the transfer function is preserved at zero frequency with a bilinear transformation, hence having the input variable prewarpf equal to zero to indicate a bilinear transformation is therefore consistent.

Examples
Create a second-order system with a resonance at 1 rad/sec.

a = [-.1,1;-1,-0.05]; 
b = [1;1]; c = [-0.5,0] 
sys = pck(a,b,c); 
minfo(sys)
system:2states1 outpus1 inputs
omega = logspace(-2,2,100); 
omega2 =[ [0.05:0.1:1.5] [1.6:.5:20] [0.9:0.01:1.1] ]; 
omega = sort([omega omega2]); 
sys_g = frsp(sys,omega);

Choose a sample frequency of 20 rads/sec and discretize the system with a bilinear transformation.

T = 2*pi/20; 
dsys = tustin(sys,T); 
dsys_g = frsp(dsys,omega,T); 
vplot('bode',sys_g,dsys_g,'-.'); 
title('Continuous system (solid), bilinear equivalent 
(dot-dash)')

The bilinear approximation is accurate up to about 2 rads/sec. This example shows the effect of choosing a higher prewarping frequency, specifically 5 rads/sec.

prewarpf = 5; 
dsys2 = tustin(sys,T,prewarpf); 
dsys2g = frsp(dsys2,omega,T); 
vplot('bode',sys_g,dsys2_g,'-.'); 
title('Continuous system (solid), tustin equivalent (dot-dash)')

Note the distortion in the frequency of the lightly damped peak. At 5 rads/sec both the continuous and discrete systems have the same transfer function.

sys_5 = vunpck(frsp(sys,5)); 
dsys2_5 = vunpck(frsp(dsys2,5,T)); 
err = abs(dsys2_5 - sys_5); 
fprintf('error at %g rad/sec is : %g ',prewarpf,err);
error at 5 rad/sec is : 1.155158e-17

This example highlights the distortion possible. If the frequency of the resonance had been critical to the design, a prewarp frequency of 1 rad/sec would have been more appropriate.

As an alternative, you can generate a filter/controller design using a warped frequency scale in the continuous domain. Then the transformation to the discrete domain would result in the correct transfer function at the frequencies of interest.

Algorithm
The prewarped tustin transformation is based on the equation:

where

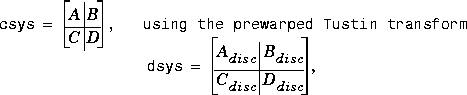
Reference
Oppenheim, A.V., and R.W. Schafer, Digital Signal Processing, Prentice Hall, New Jersey, 1975.

See Also
dtrsp, frsp, samhld, tustin

trsp, dtrsp, sdtrsp unum, xnum, ynum