

| Image Processing Toolbox |   |
Radon Transform
The radon function in the Image Processing Toolbox computes projections of an image matrix along specified directions. A projection of a two-dimensional function f(x,y) is a line integral in a certain direction. For example, the line integral of f(x,y) in the vertical direction is the projection of f(x,y) onto the x-axis; the line integral in the horizontal direction is the projection of f(x,y) onto the y-axis. Figure 7-11 shows horizontal and vertical projections for a simple two-dimensional function.
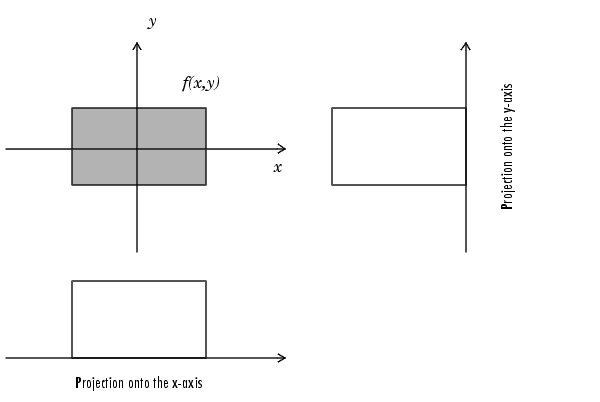
Figure 7-11: Horizontal and Vertical Projections of a Simple Function
Projections can be computed along any angle 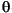 . In general, the Radon transform of f(x,y) is the line integral of f parallel to the y´ axis
. In general, the Radon transform of f(x,y) is the line integral of f parallel to the y´ axis
Figure 7-12 illustrates the geometry of the Radon transform.
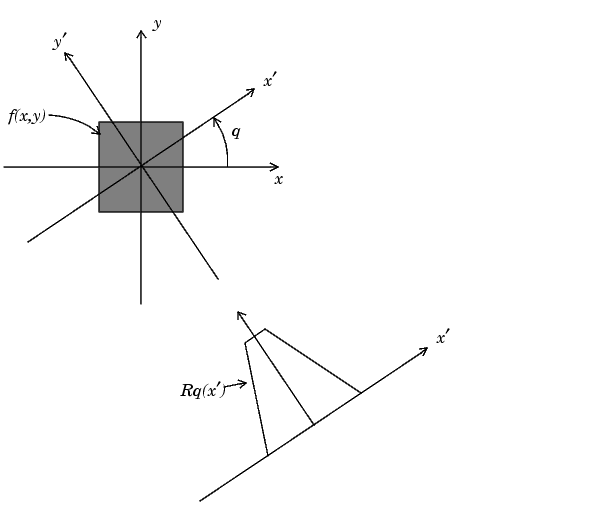
Figure 7-12: The Geometry of the Radon Transform
This command computes the Radon transform of I for the angles specified in the vector theta
[R,xp] = radon(I,theta);
The columns of R contain the Radon transform for each angle in theta. The vector xp contains the corresponding coordinates along the x´-axis. The "center pixel" of I is defined to be floor((size(I)+1)/2); this is the pixel on the x´-axis corresponding to 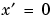 .
.
The commands below compute and plot the Radon transform at 0° and 45° of an image containing a single square object.
I = zeros(100,100); I(25:75, 25:75) = 1; imshow(I)
[R,xp] = radon(I,[0 45]); figure; plot(xp,R(:,1)); title('R_{0^o} (x\prime)') figure; plot(xp,R(:,2)); title('R_{45^o} (x\prime)')
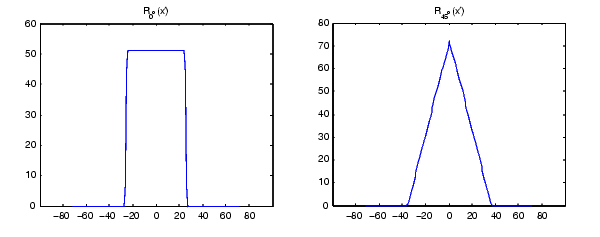
Figure 7-13: Two Radon Transforms of a Square Function
The Radon transform for a large number of angles is often displayed as an image. In this example, the Radon transform for the square image is computed at angles from 0° to 180°, in 1° increments.
theta = 0:180;
[R,xp] = radon(I,theta);
imagesc(theta,xp,R);
title('R_{\theta} (X\prime)');
xlabel('\theta (degrees)');
ylabel('X\prime');
set(gca,'XTick',0:20:180);
colormap(hot);
colorbar
Figure 7-14: A Radon Transform Using 180 Projections
 | The DCT and Image Compression | Using the Radon Transform to Detect Lines |  |