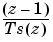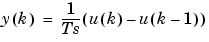| Fixed-Point Blockset |
  |
Derivative
The FixPt Derivative realization is a masked subsystem that performs discrete-time differentiation. For the this method, differentiation is approximated by the z-domain transfer function
where Ts is the sampling period. The realization is shown below.
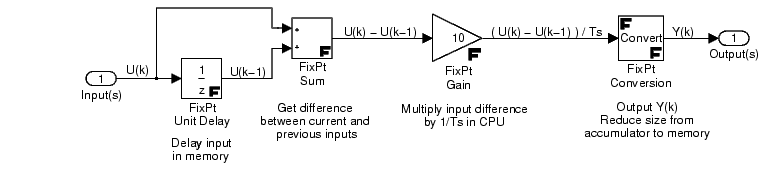
As shown in the figure, the transfer function yields the difference equation
where k is the current time step, k - 1 is the previous time step, y(k) is the current output, u(k) is the current input, and u(k - 1) is the input from the previous time step.
Parameters and Dialog Box
The dialog box and parameter descriptions for the derivative realization are given below.
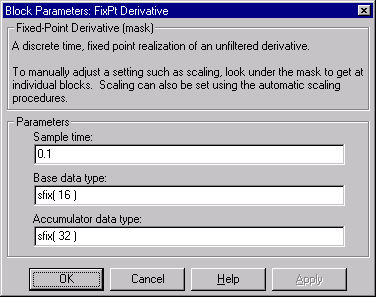
- Sample time
The time interval, Ts, between samples
- Base data type
The processor's base data type
- Accumulator data type
The processor's accumulator data type
Model Design Review
A brief review of the model design is given below. The design criteria reflect the rules presented in Design Rules.
- Using the Accumulator data type for the FixPt Sum block would rarely be advantageous. Both inputs are given by the Base data type with identical scaling so using the same data type for the output makes sense. Also, the subsequent block is a gain; and its input should be the Base data type or smaller. The input values to this block should be close so the subtraction can be safely carried out using the Base data type.
- The gain involves multiplication which is a size-growing operation. In most cases, it is desirable for gains and inputs to use the word size given by the Base data type or smaller. The output can be left at the Accumulator data type for extra precision in subsequent operations. Alternatively, if the output were stored in RAM, or used by a size-growing operation, it could be reduced to the Base data type.
- The FixPt Conversion casts the output to the Base data type before storage in RAM (before input to the unit delay).
 | Derivative Realizations | | Lead Filter or Lag Filter Realization |  |