Fixed-Point Blockset

Multiplication

The multiplication of an n-bit binary number with an m-bit binary number results in a product that is up to m + n bits in length for both signed and unsigned words. Most processors perform n-bit by n-bit multiplication and produce a 2n-bit result (double bits) assuming there is no overflow condition.

For example, the Texas Instruments TMS320C2x family of processors performs two's complement 16-bit by 16-bit multiplication and produces a 32-bit (double bit) result.

Fixed-Point Blockset Multiplication Process

Consider the multiplication of two numbers. Ideally, the real-world values obey the equation

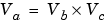
where V_b and V_c are the input values and V_a is the output value. To see how the multiplication is actually implemented, the three ideal values should be replaced by the general slope/bias encoding scheme described in Scaling.

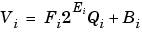
The solution of the resulting equation for the output stored integer, Q_a, is given below.

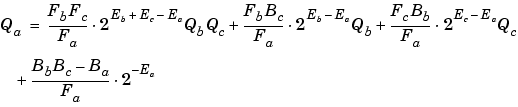
The worst-case implementation of this equation occurs when the slopes and biases of the input and output signals are mismatched. This worst-case implementation is permitted in simulation but is not always permitted for code generation since it often requires more resources than is considered practical for an embedded system. For code generation and bit-true simulations, the biases must be zero and the fractional slopes must match for most blocks. When these requirements are met, the implementation reduces to

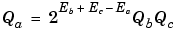
The bit-true implementation of this equation is discussed below.

Offline Conversions.   As shown in the previous section, no offline conversions are performed.

Online Conversions and Operations.   The online conversions and operations for matched slopes and biases of zero are given by these steps:

1. The integer values, Q_b and Q_c, are multiplied together.

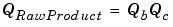
To maintain the full precision of the product, the radix point of Q_RawProduct is given by the sum of the radix points of Q_b and Q_c.

2. The previous product is converted to the output data type.

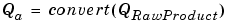
This conversion includes any necessary bit shifting, rounding, or overflow handling. Conversions are discussed in Signal Conversions.

3. Steps 1 and 2 are repeated for each additional number to be multiplied.

Example: The Multiplication Process

Suppose you want to multiply three numbers. Each of these numbers is represented by a 5-bit word, and each has a different radix point-only scaling. Additionally, the output is restricted to a 10-bit word with radix point-only scaling of 2^-4. The multiplication is shown below for the input values 5.75, 2.375, and 1.8125.

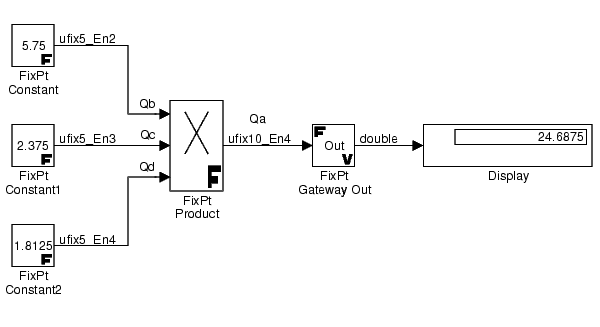
Applying the rules from the previous section, the multiplication follows these steps:

1. The first two numbers (5.75 and 2.375) are multiplied.

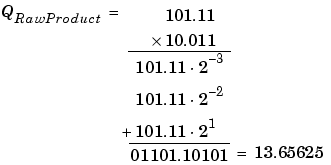
Note that the radix point of the product is given by the sum of the radix points of the multiplied numbers.

2. The result of step 1 is converted to the output data type.

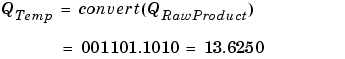
Conversions are discussed in Signal Conversions. Note that a loss in precision of one bit occurs, with the resulting value of Q_Temp determined by the rounding mode. For this example, round-to-floor is used. Furthermore, overflow did not occur but is possible for this operation.

3. The result of step 2 and the third number (1.8125) are multiplied.

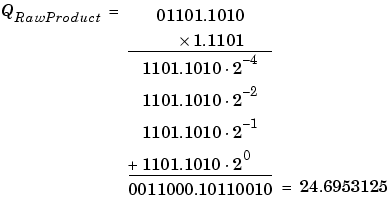
Note that the radix point of the product is given by the sum of the radix points of the multiplied numbers.

4. The product is converted to the output data type.

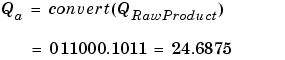
Conversions are discussed in Signal Conversions. Note that a loss in precision of four bits occurred, with the resulting value of Q_Temp determined by the rounding mode. For this example, round-to-floor is used. Furthermore, overflow did not occur but is possible for this operation.

Blocks that perform multiplication include the FixPt Product, FixPt FIR, FixPt Gain, and FixPt Matrix Gain blocks.

Addition and Subtraction

Division