Fixed-Point Blockset

Addition and Subtraction

Addition is the most common arithmetic operation a processor performs. When two n-bit numbers are added together, it is always possible to produce a result with n + 1 nonzero digits due to a carry from the leftmost digit. For two's complement addition of two numbers, there are three cases to consider:

• If both numbers are positive and the result of their addition has a sign bit of 1, then overflow has occurred; otherwise the result is correct.
• If both numbers are negative and the sign of the result is 0, then overflow has occurred; otherwise the result is correct.
• If the numbers are of unlike sign, overflow cannot occur and the result is always correct.

Fixed-Point Blockset Summation Process

Consider the summation of two numbers. Ideally, the real-world values obey the equation

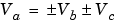
where V_b and V_c are the input values and V_a is the output value. To see how the summation is actually implemented, the three ideal values should be replaced by the general slope/bias encoding scheme described in Scaling.

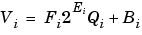
The solution of the resulting equation for the stored integer, Q_a, is given by the equation in Addition. Using shorthand notation, that equation becomes

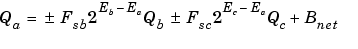
where F_sb and F_sc are the adjusted fractional slopes and B_net is the net bias. The offline conversions, and online conversions and operations are discussed below.

Offline Conversions.   F_sb, F_sc, and B_net are computed offline using round-to-nearest and saturation. Furthermore, B_net is stored using the output data type.

Online Conversions and Operations.   The remaining operations are performed online by the fixed-point processor, and depend on the slopes and biases for the input and output data types. The worst (most inefficient) case occurs when the slopes and biases are mismatched. The worst-case conversions and operations are given by these steps:

1. The initial value for Q_a is given by the net bias, B_net.

2. The first input integer value, Q_b, is multiplied by the adjusted slope, F_sb.

3. The previous product is converted to the modified output data type where the slope is one and the bias is zero.

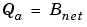
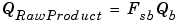
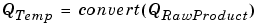
This conversion includes any necessary bit shifting, rounding, or overflow handling.

4. The summation operation is performed.

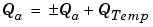
This summation includes any necessary overflow handling.

5. Steps 2 to 4 are repeated for every number to be summed.

It is important to note that bit shifting, rounding, and overflow handling are applied to the intermediate steps (3 and 4) and not to the overall sum.

Streamlining Simulations and Generated Code

If the scaling of the input and output signals is matched, the number of summation operations is reduced from the worst (most inefficient) case. For example, when an input has the same fractional slope as the output, step 2 reduces to multiplication by one and can be eliminated. Trivial steps in the summation process are eliminated for both simulation and code generation. Exclusive use of radix point-only scaling for both input signals and output signals is a common way to eliminate the occurrence of mismatched slopes and biases, and results in the most efficient simulations and generated code.

Example: The Summation Process

Suppose you want to sum three numbers. Each of these numbers is represented by an 8-bit word, and each has a different radix point-only scaling. Additionally, the output is restricted to an 8-bit word with radix point-only scaling of 2^-3.

The summation is shown below for the input values 19.875, 5.4375, and 4.84375.

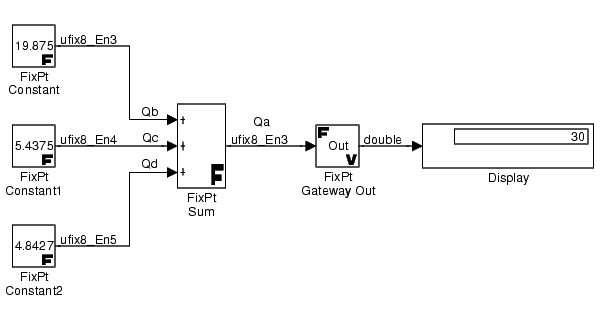
Applying the rules from the previous section, the sum follows these steps:

1. Since the biases are matched, the initial value of Q_a is trivial.

2. The first number to be summed (19.875) has a fractional slope that matches the output fractional slope. Furthermore, the radix points and storage types are identical so the conversion is trivial.

3. The summation operation is performed.

4. The second number to be summed (5.4375) has a fractional slope that matches the output fractional slope, so a slope adjustment is not needed. The storage data types also match but the difference in radix points requires that both the bits and the radix point be shifted one place to the right.

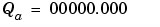
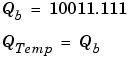
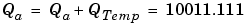
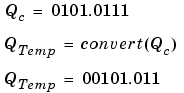
Note that a loss in precision of one bit occurs, with the resulting value of Q_Temp determined by the rounding mode. For this example, round-to-floor is used. Overflow cannot occur in this case since the bits and radix point are both shifted to the right.

5. The summation operation is performed

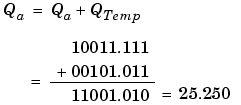
Note that overflow did not occur, but it is possible for this operation.

6. The third number to be summed (4.84375) has a fractional slope that matches the output fractional slope, so a slope adjustment is not needed. The storage data types also match but the difference in radix points requires that both the bits and the radix point be shifted two places to the right.

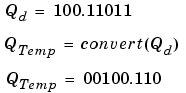
Note that a loss in precision of two bit occurs, with the resulting value of Q_Temp determined by the rounding mode. For this example, round-to-floor is used. Overflow cannot occur in this case since the bits and radix point are both shifted to the right.

7. The summation operation is performed.

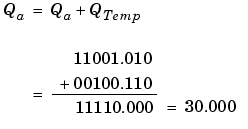
Note that overflow did not occur, but it is possible for this operation.

As shown below, the result of step 7 differs from the ideal sum.

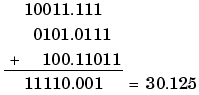
Blocks that perform addition and subtraction include the FixPt Sum, FixPt Matrix Gain, and FixPt FIR blocks.

Computational Units

Multiplication