Financial Derivatives Toolbox

Hedging with Constrained Portfolios

Both hedging functions cast the optimization as a constrained linear least squares problem. (See the function lsqlin in the Optimization Toolbox for details.) In particular, lsqlin attempts to minimize the constrained linear least squares problem

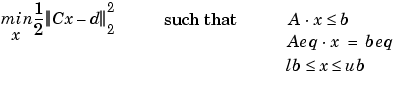
where C, A, and Aeq are matrices, and d, b, beq, lb, and ub are vectors. In all cases of interest for the Financial Derivatives Toolbox, x is a vector of asset holdings (contracts).

This section provides some examples of setting constraints and discusses how to recognize situations when the least squares problem is improperly constrained. Depending upon the constraints and the number of assets in the portfolio, a solution to a particular problem may or may not exist. Furthermore, if a solution is found, the solution may not be unique. For a unique solution to exist, the least squares problem must be sufficiently and appropriately constrained.

Example: Fully Hedged Portfolio

Recall that hedgeopt allows you to allocate an optimal hedge by one of two goals:

1. Minimize the cost of hedging a portfolio given a set of target sensitivities
2. Minimize portfolio sensitivities for a given set of maximum target costs

As an example, reproduce the results for the fully hedged portfolio example.

TargetSens = [0 0 0];
FixedInd   = [1 4 5 7 8];
[Sens,Cost,Quantity] = hedgeopt(Sensitivities,Price,Holdings,...
FixedInd,[],[],TargetSens);

Sens =
         -0.00          0.00          0.00

Cost =
      30310.85

Quantity' =
        100.00
       -227.78
        181.00
         80.00
          8.00
       -105.49
         40.00
         10.00 

This example finds a unique solution at a cost of just over $30,310. The matrix C (formed internally by hedgeopt and passed to lsqlin) is the asset Price vector expressed as a row vector.

C = Price' = [105.77 107.68 7.32 105.77 100.58 15.44 15.39 5.19]

The vector d is the current portfolio value Value0 = 25991.36. The example maintains, as closely as possible, a constant portfolio value subject to the specified constraints.

Additional Constraints.   In the absence of any additional constraints, the least squares objective involves a single equation with eight unknowns. This is an under-determined system of equations. Because such systems generally have an infinite number of solutions, you need to specify additional constraints to achieve a solution with practical significance. The additional constraints can come from two sources:

• User-specified equality constraints
• Target sensitivity equality constraints imposed by hedgeopt

The fully-hedged portfolio example specifies five equality constraints associated with holding assets 1, 4, 5, 7, and 8 fixed. This reduces the number of unknowns from eight to three, which is still an under-determined system. However, when combined with the first goal of hedgeopt, the equality constraints associated with the target sensitivities in TargetSens produce an additional system of three equations with three unknowns. This additional system guarantees that the weighted average of the delta, gamma, and vega of assets 2, 3, and 6, together with the remaining assets held fixed, satisfy the overall portfolio target sensitivity requirements in TargetSens.

Combining the least squares objective equation with the three portfolio sensitivity equations provides an overall system of four equations with three unknown asset holdings. This is no longer an under-determined system, and the solution is as shown.

If the assets held fixed are reduced, e.g., FixedInd = [1 4 5 7], hedgeopt returns a no cost, fully-hedged portfolio (Sens = [0 0 0] and Cost = 0).

If you further reduce FixedInd (e.g., [1 4 5], [1 4], or even []), hedgeopt always returns a no cost, fully-hedged portfolio. In these cases, insufficient constraints result in an under-determined system. Although hedgeopt identifies no cost, fully-hedged portfolios, there is nothing unique about them. These portfolios have little practical significance.

Constraints must be sufficient and appropriately defined. Additional constraints having no effect on the optimization are called dependent constraints. As a simple example, assume that parameter Z is constrained such that 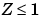. Furthermore, assume we somehow add another constraint that effectively restricts 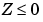. The constraint 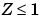now has no effect on the optimization.

Example: Minimize Portfolio Sensitivities

To illustrate using hedgeopt to minimize portfolio sensitivities for a given maximum target cost, specify a target cost of $20,000 and determine the new portfolio sensitivities, holdings, and cost of the rebalanced portfolio.

MaxCost = 20000;
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... 
Holdings, [1 4 5 7 8], [], MaxCost);

Sens =
     -10633.62      -1567.98       1415.74

Cost =
      20000.00

Quantity' =
        100.00
       -129.80
        -42.85
         80.00
          8.00
        -14.82
         40.00
         10.00

This example corresponds to the $20,000 point along the cost axis in Figure 1-1, Figure 1-2, and Figure 1-3.

When minimizing sensitivities, the maximum target cost is treated as an inequality constraint; in this case, MaxCost is the most you are willing to spend to hedge a portfolio. The least squares objective matrix C is the matrix transpose of the input asset sensitivities

C = Sensitivities'

a 3-by-8 matrix in this example, and d is a 3-by-1 column vector of zeros,
[0 0 0]'.

Without any additional constraints, the least squares objective results in an under-determined system of three equations with eight unknowns. By holding assets 1, 4, 5, 7, and 8 fixed, you reduce the number of unknowns from eight to three. Now, with a system of three equations with three unknowns, hedgeopt finds the solution shown.

Example: Under-Determined System

Reducing the number of assets held fixed creates an under-determined system with meaningless solutions. For example, see what happens with only four assets constrained.

FixedInd = [1 4 5 7];

[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... 
Holdings, FixedInd, [], MaxCost)

Sens =
         -0.00          0.00          0.00

Cost =
      20000.00

Quantity' =
        100.00
       -126.00
         71.43
         80.00
          8.00
        -65.17
         40.00
        -80.25

You have spent $20,000 (all the funds available for rebalancing) to achieve a fully-hedged portfolio.

With an increase in available funds to $50,000, you still spend all available funds to get another fully-hedged portfolio.

MaxCost  = 50000;
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, Holdings, 
FixedInd , [],MaxCost);

Sens =
         -0.00          0.00          0.00

Cost =
      50000.00

Quantity' =
        100.00
       -422.13
        390.24
         80.00
          8.00
       -182.46
         40.00
        182.34

All solutions to an under-determined system are meaningless. You buy and sell various assets to obtain zero sensitivities, spending all available funds every time. If you reduce the number of fixed assets any further, this problem is insufficiently constrained, and you find no solution (the outputs are all NaN).

Note also that no solution exists whenever constraints are inconsistent. Inconsistent constraints create an infeasible solution space; the outputs are all NaN.

Portfolio Constraints with hedgeslf

The other hedging function, hedgeslf, attempts to minimize portfolio sensitivities such that the rebalanced portfolio maintains a constant value (the rebalanced portfolio is hedged against market moves and is closest to being self-financing). If a self-financing hedge is not found, hedgeslf tries to rebalance a portfolio to minimize sensitivities.

From a least squares systems approach, hedgeslf first attempts to minimize cost in the same way that hedgeopt does. If it cannot solve this problem (a no cost, self-financing hedge is not possible), hedgeslf proceeds to minimize sensitivities like hedgeopt. Thus, the discussion of constraints for hedgeopt is directly applicable to hedgeslf as well.

Specifying Constraints with ConSet

Reference