| Control System Toolbox Function Reference | |
Compute the Padé approximation of models with time delays
Syntax
[num,den] = pade(T,N) pade(T,N) sysx = pade(sys,N) sysx = pade(sys,NI,NO,Nio)
Description
pade
approximates time delays by rational LTI models. Such approximations are useful to model time delay effects such as transport and computation delays within the context of continuous-time systems. The Laplace transform of an time delay of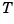 
seconds is 
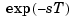. This exponential transfer function is approximated by a rational transfer function using the Padé approximation formulas [1].
[num,den] = pade(T,N)
returns the Nth-order (diagonal) Padé approximation of the continuous-time I/O delay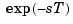 
in transfer function form. The row vectors num and den contain the numerator and denominator coefficients in descending powers of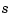 
. Both are Nth-order polynomials.
When invoked without output arguments,
pade(T,N)
plots the step and phase responses of the Nth-order Padé approximation and compares them with the exact responses of the model with I/O delay T. Note that the Padé approximation has unit gain at all frequencies.
sysx = pade(sys,N)
produces a delay-free approximation sysx of the continuous delay system sys. All delays are replaced by their Nth-order Padé approximation. See Time Delays for details on LTI models with delays.
sysx = pade(sys,NI,NO,Nio) specifies independent approximation orders for each input, output, and I/O delay. These approximation orders are given by the arrays of integers NI, NO, and Nio, such that:
NI(j) is the approximation order for the j-th input channel.NO(i) is the approximation order for the i-th output channel.Nio(i,j) is the approximation order for the I/O delay from input j to output i.You can use scalar values to specify uniform approximation orders, and [] if there are no input, output, or I/O delays.
Example
Compute a third-order Padé approximation of a 0.1 second I/O delay and compare the time and frequency responses of the true delay and its approximation. To do this, type
pade(0.1,3)
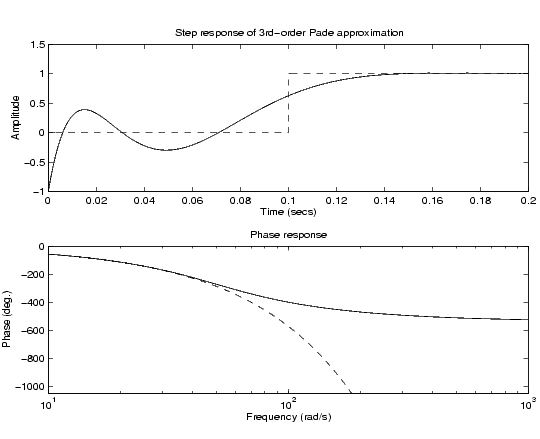
Limitations
High-order Padé approximations produce transfer functions with clustered poles. Because such pole configurations tend to be very sensitive to perturbations, Padé approximations with order N>10 should be avoided.
See Also
c2d Discretization of continuous system
delay2z Changes transfer functions of discrete-time LTI models
with delays to rational functions or absorbs FRD delays
into the frequency response phase information
References
[1] Golub, G. H. and C. F. Van Loan, Matrix Computations, Johns Hopkins University Press, Baltimore, 1989, pp. 557-558.
| | ord2 | parallel | |