

| Control System Toolbox Function Reference |   |
Form the controllability matrix
Syntax
Co = ctrb(A,B) Co = ctrb(sys)
Description
ctrb computes the controllability matrix for state-space systems. For an n-by-n matrix A and an n-by-m matrix B, ctrb(A,B) returns the controllability matrix
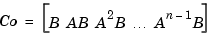
|
(0-1) |
where 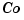 has n rows and nm columns.
has n rows and nm columns.
Co = ctrb(sys) calculates the controllability matrix of the state-space LTI object sys. This syntax is equivalent to executing
Co = ctrb(sys.A,sys.B)
The system is controllable if Co has full rank n.
Example
Check if the system with the following data
A =
1 1
4 -2
B =
1 -1
1 -1
Co=ctrb(A,B); % Number of uncontrollable states unco=length(A)-rank(Co)
unco =
1
Limitations
Estimating the rank of the controllability matrix is ill-conditioned; that is, it is very sensitive to round-off errors and errors in the data. An indication of this can be seen from this simple example.
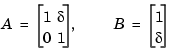
This pair is controllable if 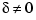 but if
but if 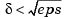 , where eps is the relative machine precision.
, where eps is the relative machine precision. ctrb(A,B) returns
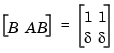
which is not full rank. For cases like these, it is better to determine the controllability of a system using ctrbf.
See Also
ctrbf Compute the controllability staircase form
obsv Compute the observability matrix
 | covar | ctrbf |  |