MATLAB Function Reference

qr

Orthogonal-triangular decomposition

Syntax

[Q,R] = qr(A)
[Q,R,E] = qr(A)
[Q,R] = qr(A,0)
[Q,R,E] = qr(A,0)
R = qr(A)          (sparse matrices)
[C,R] = qr(A,B)    (sparse matrices)
R = qr(A,0)        (sparse matrices)
[C,R] = qr(A,B,0)  (sparse matrices)
X = qr(A)

Description

The qr function performs the orthogonal-triangular decomposition of a matrix. This factorization is useful for both square and rectangular matrices. It expresses the matrix as the product of a real orthonormal or complex unitary matrix and an upper triangular matrix.

[Q,R] = qr(A) produces an upper triangular matrix R of the same dimension as A and a unitary matrix Q so that A = Q*R. For sparse matrices, Q is often nearly full.

[Q,R,E] = qr(A) produces a permutation matrix E, an upper triangular matrix R with decreasing diagonal elements, and a unitary matrix Q so that A*E = Q*R. The column permutation E is chosen so that abs(diag(R)) is decreasing.

[Q,R] = qr(A,0) and [Q,R,E] = qr(A,0) produce "economy-size" decompositions in which E is a permutation vector, so that Q*R = A(:,E). The column permutation E is chosen so that abs(diag(R)) is decreasing.

R = qr(A) for sparse matrices, produces only an upper triangular matrix, R. The matrix R provides a Cholesky factorization for the matrix associated with the normal equations,

R'*R = A'*A

This approach avoids the loss of numerical information inherent in the computation of A'*A.

[C,R] = qr(A,B) for sparse matrices, applies the orthogonal transformations to B, producing C = Q'*B without computing Q.

R = qr(A,0) and [C,R] = qr(A,B,0) for sparse matrices, produce "economy-size" results.

For sparse matrices, the Q-less QR factorization allows the solution of sparse least squares problems

with two steps

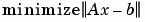
[C,R] = qr(A,b)
x = R\c

If A is sparse but not square, MATLAB uses the two steps above for the linear equation solving backslash operator, i.e., x = A\b.

X = qr(A) returns the output of the LAPACK subroutine DGEQRF or ZGEQRF. triu(qr(A)) is R.

Examples

Start with

A =
     1     2     3
     4     5     6
     7     8     9
    10    11    12

This is a rank-deficient matrix; the middle column is the average of the other two columns. The rank deficiency is revealed by the factorization:

[Q,R] = qr(A)

Q =

    -0.0776    -0.8331     0.5444     0.0605
    -0.3105    -0.4512    -0.7709     0.3251
    -0.5433    -0.0694    -0.0913    -0.8317
    -0.7762     0.3124     0.3178     0.4461

R =

    -12.8841    -14.5916    -16.2992
           0     -1.0413     -2.0826
           0           0      0.0000
           0           0           0

The triangular structure of R gives it zeros below the diagonal; the zero on the diagonal in R(3,3) implies that R, and consequently A, does not have full rank.

The QR factorization is used to solve linear systems with more equations than unknowns. For example

b =

    1
    3
    5
    7

The linear system Ax = b represents four equations in only three unknowns. The best solution in a least squares sense is computed by

x = A\b

which produces

Warning: Rank deficient, rank = 2, tol = 1.4594E-014
x =
    0.5000
          0
    0.1667

The quantity tol is a tolerance used to decide if a diagonal element of R is negligible. If [Q,R,E] = qr(A), then

tol = max(size(A))*eps*abs(R(1,1))

The solution x was computed using the factorization and the two steps

y = Q'*b;
x = R\y

The computed solution can be checked by forming Ax. This equals b to within roundoff error, which indicates that even though the simultaneous equations Ax = b are overdetermined and rank deficient, they happen to be consistent. There are infinitely many solution vectors x; the QR factorization has found just one of them.

Algorithm

The qr function uses LAPACK routines to compute the QR decomposition:

Syntax	Real	Complex
R = qr(A) R = qr(A,0)	DGEQRF	ZGEQRF
[Q,R] = qr(A) [Q,R] = qr(A,0)	DGEQRF, DORGQR	ZGEQRF, ZUNGQR
[Q,R,e] = qr(A) [Q,R,e] = qr(A,0)	DGEQPF, DORGQR	ZGEQPF, ZUNGQR

See Also

lu, null, orth, qrdelete, qrinsert

The arithmetic operators \ and /

References

[1]  Anderson, E., Z. Bai, C. Bischof, S. Blackford, J. Demmel, J. Dongarra, J. Du Croz, A. Greenbaum, S. Hammarling, A. McKenney, and D. Sorensen, LAPACK User's Guide, Third Edition, SIAM, Philadelphia, 1999.

qmr

qrdelete