delaunay (MATLAB Function Reference)

Delaunay triangulation

Syntax

TRI = delaunay(x,y)
TRI = delaunay(x,y,'sorted')

Definition

Given a set of data points, the Delaunay triangulation is a set of lines connecting each point to its natural neighbors. The Delaunay triangulation is related to the Voronoi diagram-- the circle circumscribed about a Delaunay triangle has its center at the vertex of a Voronoi polygon.

Description

TRI = delaunay(x,y) returns a set of triangles such that no data points are contained in any triangle's circumscribed circle. Each row of the m-by-3 matrix TRI defines one such triangle and contains indices into the vectors x and y.

To avoid the degeneracy of collinear data, delaunay adds some random fuzz to the data. The default fuzz standard deviation 4*sqrt(eps) has been chosen to maintain about seven digits of accuracy in the data.

tri = delaunay(x,y,fuzz) uses the specified value for the fuzz standard deviation. It is possible that no value of fuzz produces a correct triangulation. In this unlikely situation, you need to preprocess your data to avoid collinear or nearly collinear data.

TRI = delaunay(x,y,'sorted') assumes that the points x and y are sorted first by y and then by x and that duplicate points have already been eliminated.

Remarks

The Delaunay triangulation is used with: griddata (to interpolate scattered data), convhull, voronoi (to compute the voronoi diagram), and is useful by itself to create a triangular grid for scattered data points.

The functions dsearch and tsearch search the triangulation to find nearest neighbor points or enclosing triangles, respectively.

Note delaunay is based on qhull [1]. For information about qhull, see http://www.geom.umn.edu/software/qhull/. For copyright information, see http://www.geom.umn.edu/software/download/COPYING.html.

Examples

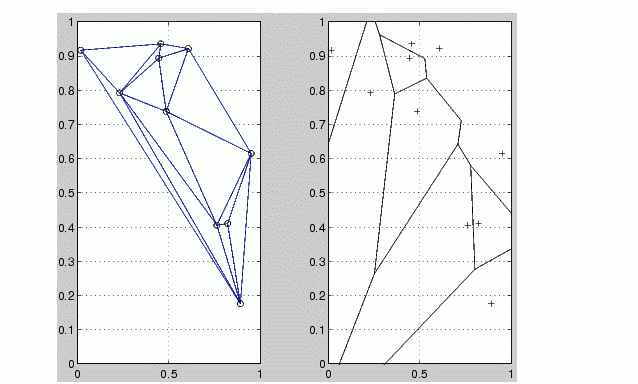
This code plots the Delaunay triangulation for 10 randomly generated points.

rand('state',0);
x = rand(1,10); 
y = rand(1,10); 
TRI = delaunay(x,y);
subplot(1,2,1),...
trimesh(TRI,x,y,zeros(size(x))); view(2),...
axis([0 1 0 1]); hold on; 
plot(x,y,'o');
set(gca,'box','on');

Compare the Voronoi diagram of the same points:

[vx, vy] = voronoi(x,y,TRI);
subplot(1,2,2),...
plot(x,y,'r+',vx,vy,'b-'),...
axis([0 1 0 1])

See Also

convhull, delaunay3, delaunayn, dsearch, griddata, trimesh, trisurf, tsearch, voronoi, voronoin

References

[1] National Science and Technology Research Center for Computation and Visualization of Geometric Structures (The Geometry Center), University of Minnesota. 1993.

del2 delaunay3