MATLAB Function Reference

besselh

Bessel functions of the third kind (Hankel functions)

Syntax

H = besselh(nu,K,Z)
H = besselh(nu,Z)
H = besselh(nu,1,Z,1)
H = besselh(nu,2,Z,1)
[H,ierr] = besselh(...) 

Definitions

The differential equation

where 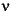is a nonnegative constant, is called Bessel's equation, and its solutions are known as Bessel functions. 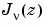and 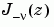form a fundamental set of solutions of Bessel's equation for noninteger 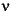. 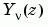is a second solution of Bessel's equation--linearly independent of 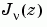-- defined by:

The relationship between the Hankel and Bessel functions is:

Description

H = besselh(nu,K,Z) for K = 1 or 2 computes the Hankel functions

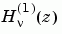or

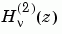for each element of the complex array Z. If nu and Z are arrays of the same size, the result is also that size. If either input is a scalar, it is expanded to the other input's size. If one input is a row vector and the other is a column vector, the result is a two-dimensional table of function values.

H = besselh(nu,Z) uses K = 1.

H = besselh(nu,1,Z,1) scales

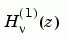by exp(-i*z).

H = besselh(nu,2,Z,1) scales

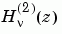by exp(+i*z).

[H,ierr] = besselh(...) also returns an array of error flags:

ierr = 1	Illegal arguments.
ierr = 2	Overflow. Return Inf.
ierr = 3	Some loss of accuracy in argument reduction.
ierr = 4	Unacceptable loss of accuracy, Z or nu too large.
ierr = 5	No convergence. Return NaN.

beep

besseli, besselk