Mathematics

Representing ODE Problems

This section describes the process for solving initial value ODE problems using one of the MATLAB ODE solvers. It uses the van der Pol equation:

• To describe the steps needed to solve an ODE problem using MATLAB
• As an example of a stiff ODE problem

Note    See ODE Solver Basic Syntax for more information.

Example: Solving an IVP ODE in MATLAB (van der Pol Equation, Nonstiff)

This example explains and illustrates the steps you need to solve an initial value ODE problem using MATLAB.

1 Rewrite the Problem as a System of First-Order ODEs.   ODEs often involve a number of dependent variables, as well as derivatives of order higher than one. To use the MATLAB ODE solvers, you must rewrite such equations as an equivalent system of first-order differential equations of the form

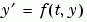
You can write any ordinary differential equation

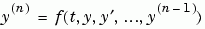
as a system of first-order equations by making the substitutions

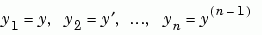
The result is an equivalent system of 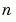first-order ODEs.

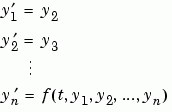
For example, you can rewrite the van der Pol equation (second-order)

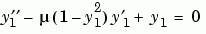
where 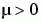is a scalar parameter, by making the substitution 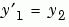. The resulting system of first-order ODEs is

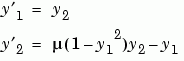
2 Code the System of First-Order ODEs in MATLAB.    Once you represent the equation as a system of first-order ODEs, you can code it as a function that a MATLAB ODE solver can use. The function must be of the form

dydt = odefun(t,y)

Although t and y must be the function's first two arguments, the function does not need to use them. The output dydt, a column vector, is the derivative of y.

The code below represents the van der Pol system in a MATLAB function, vdp1. The vdp1 function assumes that 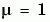. 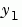and 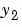become elements y(1) and y(2) of a two-element vector.

function dydt = vdp1(t,y)
dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

Note that, although vdp1 must accept the arguments t and y, it does not use t in its computations.

3 Apply a Solver to the Problem.   Decide which solver you want to use to solve the problem. Then call the solver and pass it the function you created to describe the first-order system of ODEs, the time interval on which you want to solve the problem, and an initial condition vector. See Initial Value Problem Solvers and the ODE solver reference page for descriptions of the ODE solvers.

For the van der Pol system, you can use ode45 on time interval [0 20] with initial values y(1) = 2 and y(2) = 0.

[t,y] = ode45(@vdp1,[0 20],[2; 0]);

This example uses @ to pass vdp1 as a function handle to ode45. The resulting output is a column vector of time points t and a solution array y. Each row in y corresponds to a time returned in the corresponding row of t. The first column of y corresponds to 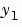, and the second column to .

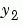Note    See the function_handle (@), func2str, and str2func reference pages, and the Function Handles chapter of "Programming and Data Types" in the MATLAB documentation for information about function handles.

4 View the Solver Output.   You can simply use the plot command to view the solver output.

plot(t,y(:,1),'-',t,y(:,2),'--')
title('Solution of van der Pol Equation, \mu = 1');
xlabel('time t');
ylabel('solution y');
legend('y_1','y_2')

As an alternative, you can use a solver output function to process the output. The solver calls the function specified in the integration property OutputFcn after each successful time step. Use odeset to set OutputFcn to the desired function. See OutputFcn for more information.

Passing Additional Parameters to an ODE Function.   The solver passes any input parameters that follow the options argument to the ODE function and any function you specify in options. For example:

1. Generalize the van der Pol function by passing it a mu parameter, instead of specifying a value for mu explicitly in the code.

function dydt = vdp1(t,y,mu)
dydt = [y(2); mu*(1-y(1)^2)*y(2)-y(1)];

2. Pass the parameter mu to the function vdp1 by specifying it after the options argument in the call to the solver. This example uses options = [] as a placeholder.

[t,y] = ode45(@vdp1,tspan,y0,[],mu)

calls

vdp1(t,y,mu)

See vdpode for a complete example based on these functions.

Example: The van der Pol Equation, µ = 1000 (Stiff)

Note    For detailed instructions for solving an initial value ODE problem in MATLAB, see Example: Solving an IVP ODE in MATLAB (van der Pol Equation, Nonstiff).

This example presents a stiff problem. For a stiff problem, solutions can change on a time scale that is very short compared to the interval of integration, but the solution of interest changes on a much longer time scale. Methods not designed for stiff problems are ineffective on intervals where the solution changes slowly because they use time steps small enough to resolve the fastest possible change.

When 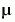is increased to 1000, the solution to the van der Pol equation changes dramatically and exhibits oscillation on a much longer time scale. Approximating the solution of the initial value problem becomes a more difficult task. Because this particular problem is stiff, a solver intended for nonstiff problems, such as ode45, is too inefficient to be practical. A solver such as ode15s is intended for such stiff problems.

The vdp1000 function evaluates the van der Pol system with 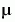= 1000.

function dydt = vdp1000(t,y)
dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];

Note    This example hardcodes 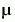in the ODE function. The vdpode example solves the same problem, but passes a user-specified 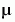as an additional argument to the ODE function. See Additional ODE Solver Arguments.

Now use the ode15s function to solve the problem with the initial condition vector of [2; 0], but a time interval of [0 3000]. For scaling purposes, plot just the first component of y(t).

[t,y] = ode15s(@vdp1000,[0 3000],[2; 0]);
plot(t,y(:,1),'-');
title('Solution of van der Pol Equation, \mu = 1000');
xlabel('time t');
ylabel('solution y_1');

Initial Value Problem Solvers

Improving ODE Solver Performance