

| Mathematics |   |
Representing PDE Problems
pdepeExample: A Single PDE
This example illustrates the straightforward formulation, solution, and plotting of the solution of a single PDE
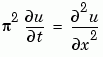
This equation holds on an interval 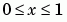 for times
for times 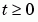 . At
. At 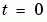 , the solution satisfies the initial condition
, the solution satisfies the initial condition
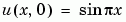
At 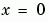 and
and 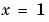 , the solution satisfies the boundary conditions
, the solution satisfies the boundary conditions
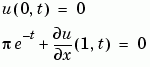
Note
The demo pdex1 contains the complete code for this example. The demo uses subfunctions to place all functions it requires in a single M-file. To run the demo type pdex1 at the command line. See PDE Solver Basic Syntax for more information.
|
1 Rewrite the PDE. Write the PDE in the form
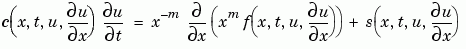
This is the form shown in Equation 15-3 and expected by pdepe. See Introduction to PDE Problems for more information. For this example, the resulting equation is
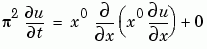
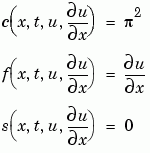
2 Code the PDE in MATLAB. Once you rewrite the PDE in the form shown above (Equation 15-3) and identify the terms, you can code the PDE in a function that pdepe can use. The function must be of the form
[c,f,s] = pdefun(x,t,u,dudx)
where c, f, and s correspond to the 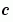 ,
, 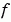 , and
, and 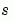 terms. The code below computes
terms. The code below computes c, f, and s for the example problem.
function [c,f,s] = pdex1pde(x,t,u,DuDx) c = pi^2; f = DuDx; s = 0;
3 Code the Initial Conditions Function. You must code the initial conditions in a MATLAB function of the form
u = icfun(x)
The code below represents the initial conditions in the MATLAB function pdex1ic.
function u0 = pdex1ic(x) u0 = sin(pi*x);
4 Code the Boundary Conditions Function. You must also code the boundary conditions in a MATLAB function of the form
[pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)
The boundary conditions, written in the same form as Equation 15-5, are
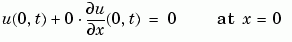
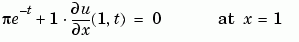
The code below evaluates the components 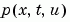 and
and 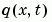 of the boundary conditions in the MATLAB function
of the boundary conditions in the MATLAB function pdex1bc.
function [pl,ql,pr,qr] = pdex1bc(xl,ul,xr,ur,t) pl = ul; ql = 0; pr = pi * exp(-t); qr = 1;
In the function pdex1bc, pl and ql correspond to the left boundary conditions (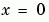 ), and
), and pr and qr correspond to the right boundary condition (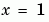 ).
).
5 Select Mesh Points for the Solution. Before you use the MATLAB PDE solver, you need to specify the mesh points 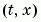 at which you want
at which you want pdepe to evaluate the solution. Specify the points as vectors t and x.
The vectors t and x play different roles in the solver (see MATLAB Partial Differential Equation Solver). In particular, the cost and the accuracy of the solution depend strongly on the length of the vector x. However, the computation is much less sensitive to the values in the vector t.
This example requests the solution on the mesh produced by 20 equally spaced points from the spatial interval [0,1] and five values of t from the time interval [0,2].
x = linspace(0,1,20); t = linspace(0,2,5);
6 Apply the PDE Solver. The example calls pdepe with m = 0, the functions pdex1pde, pdex1ic, and pdex1bc, and the mesh defined by x and t at which pdepe is to evaluate the solution. The pdepe function returns the numerical solution in a three-dimensional array sol, where sol(i,j,k) approximates the kth component of the solution, 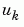 , evaluated at
, evaluated at t(i) and x(j).
m = 0; sol = pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
This example uses @ to pass pdex1pde, pdex1ic, and pdex1bc as function handles to pdepe.
Note
See the function_handle (@), func2str, and str2func reference pages, and the Function Handles chapter of "Programming and Data Types" in the MATLAB documentation for information about function handles.
|
7 View the Results. Complete the example by displaying the results:
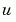 has only one component, but for illustrative purposes, the example "extracts" it from the three-dimensional array. The surface plot shows the behavior of the solution.
has only one component, but for illustrative purposes, the example "extracts" it from the three-dimensional array. The surface plot shows the behavior of the solution.u = sol(:,:,1);
surf(x,t,u)
title('Numerical solution computed with 20 mesh points')
xlabel('Distance x')
ylabel('Time t')
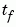 , the final value of
, the final value of 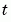 . In this example,
. In this example, 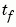
= t = 2. See Evaluating the Solution at Specific Points for more information.figure
plot(x,u(end,:))
title('Solution at t = 2')
xlabel('Distance x')
ylabel('u(x,2)')
Evaluating the Solution at Specific Points
After obtaining and plotting the solution above, you might be interested in a solution profile for a particular value of t, or the time changes of the solution at a particular point x. The kth column u(:,k) (of the solution extracted in step 7) contains the time history of the solution at x(k). The jth row u(j,:) contains the solution profile at t(j).
Using the vectors x and u(j,:), and the helper function pdeval, you can evaluate the solution u and its derivative 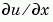 at any set of points
at any set of points xout
[uout,DuoutDx] = pdeval(m,x,u(j,:),xout)
The example pdex3 uses pdeval to evaluate the derivative of the solution at xout = 0. See pdeval for details.
 | MATLAB Partial Differential Equation Solver | Improving PDE Solver Performance |  |