

| Mathematics |   |
Matrix Powers and Exponentials
This section tells you how to obtain the following matrix powers and exponentials in MATLAB:
Positive Integer Powers
If A is a square matrix and p is a positive integer, then A^p multiplies A by itself p times.
X = A^2
X =
3 6 10
6 14 25
10 25 46
Inverse and Fractional Powers
If A is square and nonsingular, then A^(-p) multiplies inv(A) by itself p times.
Y = B^(-3)
Y =
0.0053 -0.0068 0.0018
-0.0034 0.0001 0.0036
-0.0016 0.0070 -0.0051
Fractional powers, like A^(2/3), are also permitted; the results depend upon the distribution of the eigenvalues of the matrix.
Element-by-Element Powers
The .^ operator produces element-by-element powers. For example,
X = A.^2
A =
1 1 1
1 4 9
1 9 36
Exponentials
sqrtm(A)
computes A^(1/2) by a more accurate algorithm. The m in sqrtm distinguishes this function from sqrt(A) which, like A.^(1/2), does its job element-by-element.
A system of linear, constant coefficient, ordinary differential equations can be written
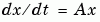
where x = x(t) is a vector of functions of t and A is a matrix independent of t. The solution can be expressed in terms of the matrix exponential,
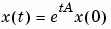
expm(A)
computes the matrix exponential. An example is provided by the 3-by-3 coefficient matrix
A =
0 -6 -1
6 2 -16
-5 20 -10
and the initial condition, x(0)
x0 =
1
1
1
The matrix exponential is used to compute the solution, x(t), to the differential equation at 101 points on the interval 0 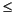 t
t 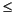 1 with
1 with
X = []; for t = 0:.01:1 X = [X expm(t*A)*x0]; end
A three-dimensional phase plane plot obtained with
plot3(X(1,:),X(2,:),X(3,:),'-o')
shows the solution spiraling in towards the origin. This behavior is related to the eigenvalues of the coefficient matrix, which are discussed in the next section.
 | QR Factorization | Eigenvalues |  |