

| Wavelet Toolbox |   |
Wavelet packet decomposition 2-D.
Syntax
T = wpdec2(X,N,'wname',E,P) T = wpdec2(X,N,'wname')
Description
wpdec2 is a two-dimensional wavelet packet analysis function.
T = wpdec2(X,N,'wname',E,P) returns a wavelet packet tree T corresponding to the wavelet packet decomposition of the matrix X, at level N, with a particular wavelet ('wname', see wfilters for more information).
E is a string containing the type of entropy (see wentropy for more information):
E = 'shannon', 'threshold', 'norm', 'log energy', 'sure', 'user'
'shannon' or 'log energy': P is not used
'threshold' or 'sure': P is the threshold (0 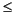
P)
'user': P is a string containing the name of a user-defined function.
T = wpdec2(X,N,'wname') is equivalent to
T = wpdec2(X,N,'wname','shannon').
See wpdec for a more complete description of the wavelet packet decomposition.
Examples
% The current extension mode is zero-padding (see dwtmode).
% Load image.
load tire
% X contains the loaded image.
% For an image the decomposition is performed using:
t = wpdec2(X,2,'db1');
% The default entropy is shannon.
% Plot wavelet packet tree
% (quarternary tree, or tree of order 4).
plot(t)
Algorithm
The algorithm used for the wavelet packets decomposition follows the same line as the wavelet decomposition process (see dwt2 and wavedec2 for more information).
See Also
wavedec2, waveinfo, wentropy, wpdec, wprec2
References
Coifman, R.R.; M.V. Wickerhauser (1992), "Entropy-based algorithms for best basis selection," IEEE Trans. on Inf. Theory, vol. 38, 2, pp. 713-718.
Meyer, Y. (1993), Les ondelettes. Algorithmes et applications, Colin Ed., Paris, 2nd edition. (English translation: Wavelets: Algorithms and Applications, SIAM).
Wickerhauser, M.V. (1991), "INRIA lectures on wavelet packet algorithms," Proceedings ondelettes et paquets d'ondes 17-21 June Rocquencourt France, pp. 31-99.
Wickerhauser, M.V. (1994), Adapted wavelet analysis from theory to software Algorithms, A.K. Peters.
 | wpdec | wpdencmp |  |