Wavelet Toolbox

Choosing the Optimal Decomposition

Based on the organization of the wavelet packet library, it is natural to count the decompositions issued from a given orthogonal wavelet.

A signal of length N = 2L can be expanded in 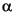different ways, where 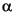is the number of binary subtrees of a complete binary tree of depth L. As a result, 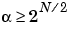(see [Mal98] page 323).

As this number may be very large, and since explicit enumeration is generally unmanageable, it is interesting to find an optimal decomposition with respect to a convenient criterion, computable by an efficient algorithm. We are looking for a minimum of the criterion.

Functions verifying an additivity-type property are well-suited for efficient searching of binary-tree structures and the fundamental splitting. Classical entropy-based criteria match these conditions and describe information- related properties for an accurate representation of a given signal. Entropy is a common concept in many fields, mainly in signal processing. Let us list four different entropy criteria (see [CoiW92]), many others are available and can be easily integrated (type help wentropy). In the following expressions s is the signal and (s_i) are the coefficients of s in an orthonormal basis.

The entropy E must be an additive cost function such that E(0) = 0 and

• The (nonnormalized) Shannon entropy

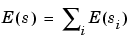
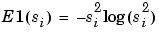
so

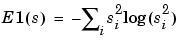
with the convention 0log(0) = 0

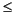• The concentration in l^p norm with 1 p

so

• The logarithm of the "energy" entropy

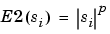
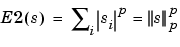
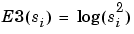
so

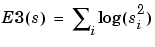
with the convention log(0) = 0.

• The threshold entropy

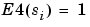if 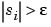and 0 elsewhere, so 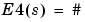{i such that 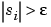} is the number of time instants when the signal is greater than a threshold .

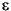These entropy functions are available using the wentropy M-file.

Example 1: Compute Various Entropies.   

1. Generate a signal of energy equal to 1.

   s = ones(1,16)*0.25;
   

2. Compute the Shannon entropy of s.

   e1 = wentropy(s,'shannon')
       e1 = 2.7726
   

3. Compute the l^1.5 entropy of s, equivalent to norm(s,1.5)^1.5.

   e2 = wentropy(s,'norm',1.5)
       e2 = 2
   

4. Compute the "log energy" entropy of s.

   e3 = wentropy(s,'log energy')
       e3 = -44.3614
   

5. Compute the threshold entropy of s, using a threshold value of 0.24.

   e4 = wentropy(s,'threshold', 0.24)
       e4 = 16
   

Example 2: Minimum-Entropy Decomposition.   

This simple example illustrates the use of entropy to determine whether a new splitting is of interest to obtain a minimum-entropy decomposition.

1. We start with a constant original signal. Two pieces of information are
   sufficient to define and to recover the signal (i.e., length and constant value).

   w00 = ones(1,16)*0.25;
   

2. Compute entropy of original signal.

   e00 = wentropy(w00,'shannon')
       e00 = 2.7726
   

3. Then split w00 using the haar wavelet.

   [w10,w11] = dwt(w00,'db1');
   

4. Compute entropy of approximation at level 1

   e10 = wentropy(w10,'shannon')
       e10 = 2.0794
   

The detail of level 1, w11, is zero; the entropy e11 is zero. Due to the additivity property the entropy of decomposition is given by e10+e11=2.0794. This has to be compared to the initial entropy e00=2.7726. We have e10 + e11 < e00, so the splitting is interesting.

5. Now split w10 (not w11 because the splitting of a null vector is without interest since the entropy is zero).

   [w20,w21] = dwt(w10,'db1');
   

6. We have w20=0.5*ones(1,4) and w21 is zero. The entropy of the approximation level 2 is:

   e20 = wentropy(w20,'shannon')
       e20 = 1.3863
   

Again we have e20 + 0 < e10, so splitting makes the entropy decrease.

7. Then

   [w30,w31] = dwt(w20,'db1');
   e30 = wentropy(w30,'shannon')
       e30 = 0.6931
   
   [w40,w41] = dwt(w30,'db1')
       w40 = 1.0000
       w41 = 0
   
   e40 = wentropy(w40,'shannon')
       e40 = 0
   

In the last splitting operation we find that only one piece of information is needed to reconstruct the original signal. The wavelet basis at level 4 is a best basis according to Shannon entropy (with null optimal entropy since e40+e41+e31+e21+e11 = 0).

8. Perform wavelet packets decomposition of the signal s defined in example 1.

   t = wpdec(s,4,'haar','shannon');
   

The wavelet packet tree below shows the nodes labeled with original entropy numbers.

Figure 6-42: Entropy Values

9. Now compute the best tree.

   bt = besttree(t);
   

The best tree is displayed in the figure below. In this case, the best tree corresponds to the wavelet tree. The nodes are labeled with optimal entropy.

Figure 6-43: Optimal Entropy Values

Organizing the Wavelet Packets

Some Interesting Subtrees