Wavelet Toolbox    

Compressing an Image Using Wavelet Packets

  1. Click the Compress button to bring up the Wavelet Packet 2-D Compression window. Select the Bal. sparsity-norm (sqrt) option from the Select thresholding method menu.

    Notice that the default threshold (7.125) provides about 64% compression while retaining virtually all the energy of the original image. Depending on your criteria, it may be worthwhile experimenting with more aggressive thresholds to achieve a higher degree of compression. Recall that we are not doing any quantization of the image, merely setting specific coefficients to zero. This can be considered a pre-compression step in a broader compression system.

  1. Alter the threshold: type the number 30 in the text field opposite the threshold slider located on the right side of the Wavelet Packet 2-D Compression window. Then press the Enter key.

    Setting all wavelet packet coefficients whose value falls below 30 to zero yields much better results. Note that the new threshold achieves around 92% of zeros, while still retaining nearly 98% of the image energy. Compare this wavelet packet analysis to the wavelet analysis of the same image in Compressing Images.

  1. Click the Compress button to start the compression.

    You can see the result obtained by wavelet packet coefficients thresholding and image reconstruction. The visual recovery is correct, but not perfect. The compressed image, shown side-by-side with the original, shows some artifacts.

  1. Click the Close button located at the bottom of the Wavelet Packet 2-D Compression window. Update the synthesized image by clicking Yes when the dialog box appears.

Take this opportunity to try out your own compression strategy. Adjust the threshold value, the entropy function, and the wavelet, and see if you can obtain better results.

Hint: The bior6.8 wavelet is better suited to this analysis than is haar, and can lead to a better compression ratio. When a biorthogonal wavelet is used, then instead of "Retained energy" the information displayed is "Energy ratio." For more information, see Compression Scores on page 6-108.

Before concluding this analysis, it is worth turning our attention to the "colored coefficients for terminal nodes plot" and considering the best tree decomposition for this image.

This plot is shown in the lower right side of the Wavelet Packet 2-D tool. The plot shows us which details have been decomposed and which have not. Larger squares represent details that have not been broken down to as many levels as smaller squares. Consider, for example, this level 2 decomposition pattern:

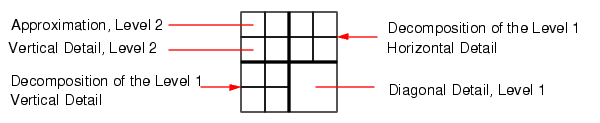
Looking at the pattern of small and large squares in the fingerprint analysis shows that the best tree algorithm has apparently singled out the diagonal details, often sparing these from further decomposition. Why is this?

If we consider the original image, we realize that much of its information is concentrated in the sharp edges that constitute the fingerprint's pattern. Looking at these edges, we see that they are predominantly oriented horizontally and vertically. This explains why the best tree algorithm has "chosen" not to decompose the diagonal details -- they do not provide very much information.


 Two-Dimensional Wavelet Packet Analysis Importing and Exporting from Graphical Tools