| Wavelet Toolbox | |
Discussion
For the db2 analysis, the details for levels 2 to 4 show a periodic form that is very regular, and that increases with the level. This is explained by the fact that the detail for level j takes into account primarily the fluctuations of the polynomial function around its mean value on dyadic intervals that are 2j long. The fluctuations are periodic and very large in relation to the details of the noise decomposition.
On the other hand, for the db3 analysis, we find the presence of white noise thus indicating that the polynomial does not come into play in any of the details. The wavelet suppresses the polynomial part and analyzes the noise.
Suppressing part of a signal allows us to highlight the remainder.
Vanishing Moments
The ability of a wavelet to suppress a polynomial depends on a crucial mathematical characteristic of the wavelet called its number of vanishing moments. A technical discussion of vanishing moments appears in the sections Frequently Asked Questions and Wavelet Families: Additional Discussion. For the present discussion, it suffices to think of "moment" as an extension of "average." Since a wavelet's average value is zero, it has (at least) one vanishing moment.
More precisely, if the average value of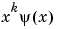 
is zero (where
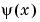is the wavelet function), for 
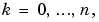then the wavelet has 
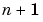vanishing moments and polynomials of degree n are suppressed by this wavelet.
| | Suppressing Signals | De-Noising Signals | |