Wavelet Toolbox

The Continuous Wavelet Transform

Mathematically, the process of Fourier analysis is represented by the Fourier transform:

which is the sum over all time of the signal f(t) multiplied by a complex exponential. (Recall that a complex exponential can be broken down into real and imaginary sinusoidal components.)

The results of the transform are the Fourier coefficients 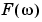, which when multiplied by a sinusoid of frequency 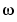, yield the constituent sinusoidal components of the original signal. Graphically, the process looks like:

Similarly, the continuous wavelet transform (CWT) is defined as the sum over all time of the signal multiplied by scaled, shifted versions of the wavelet function :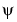

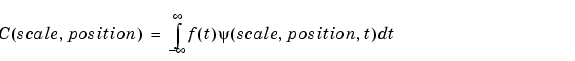
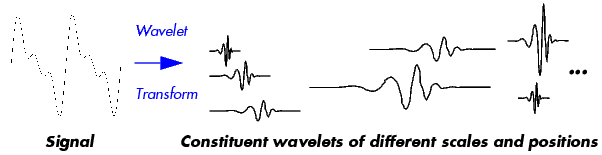
The result of the CWT are many wavelet coefficients C, which are a function of scale and position.

Multiplying each coefficient by the appropriately scaled and shifted wavelet yields the constituent wavelets of the original signal:

Number of Dimensions

Scaling