

| Symbolic Math Toolbox |   |
Syntax
hypergeom(n, d, z)
Description
hypergeom(n, d, z) is the generalized hypergeometric function F(n, d, z), also known as the Barnes extended hypergeometric function and denoted by jFk where j = length(n) and k = length(d). For scalar a, b, and c, hypergeom([a,b],c,z) is the Gauss hypergeometric function 2F1(a,b;c;z).
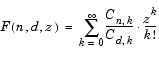
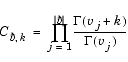
hypergeom([],[],z) returns exp(z)
hypergeom(1,[],z) returns -1/(-1+z)
hypergeom(1,2,'z') returns (exp(z)-1)/z
hypergeom([1,2],[2,3],'z') returns -2*(-exp(z)+1+z)/z^2
hypergeom(a,[],z) returns (1-z)^(-a)
hypergeom([],1,-z^2/4) returns besselj(0,z)
hypergeom([-n, n],1/2,(1-z)/2) returns
expand(cos(n*acos(z)))
n-th Chebyshev polynomial.
 | horner | ifourier |  |