Statistics Toolbox

F Distribution

The following sections provide an overview of the F distribution.

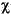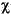Background of the F distribution.   The F distribution has a natural relationship with the chi-square distribution. If ₁ and ₂ are both chi-square with 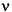₁ and 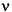₂ degrees of freedom respectively, then the statistic F below is F distributed.

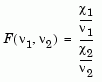
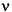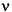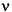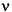The two parameters, ₁ and ₂, are the numerator and denominator degrees of freedom. That is, ₁ and ₂ are the number of independent pieces information used to calculate 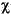₁ and 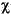₂ respectively.

Definition of the F distribution.   The pdf for the F distribution is

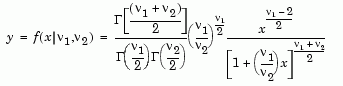
where 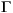( · ) is the Gamma function.

Example and Plot of the F distribution.   The most common application of the F distribution is in standard tests of hypotheses in analysis of variance and regression.

The plot shows that the F distribution exists on the positive real numbers and is skewed to the right.

x = 0:0.01:10;
y = fpdf(x,5,3);
plot(x,y)

Exponential Distribution

Noncentral F Distribution