| Statistics Toolbox | |
Normal probability density function (pdf).
Syntax
Y = normpdf(X,MU,SIGMA)
Description
normpdf(X,MU,SIGMA)
computes the normal pdf at each of the values in X using the corresponding parameters in MU and SIGMA. Vector or matrix inputs for X, MU, and SIGMA must all have the same size. A scalar input is expanded to a constant matrix with the same dimensions as the other inputs. The parameters in SIGMA must be positive.
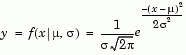
The likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a fixed value of x.
The standard normal distribution has µ = 0 and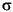 
= 1.
If x is standard normal, then x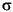 + µ is also normal with mean µ and standard deviation 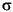. Conversely, if y is normal with mean µ and standard deviation 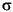, then x = (y-µ) / 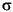is standard normal.
Examples
mu = [0:0.1:2];
[y i] = max(normpdf(1.5,mu,1));
MLE = mu(i)
MLE =
1.5000
See Also
normfit, normfit, norminv, normplot, normrnd, normspec, normstat, pdf
| | norminv | normplot | |