| Statistics Toolbox | |
Kolmogorov-Smirnov test to compare the distribution of two samples.
Syntax
H = kstest2(X1,X2) H = kstest2(X1,X2,alpha,tail) [H,P,KSSTAT] = kstest(X,cdf,alpha,tail)
Description
H = kstest2(X1,X2)
X1 and X2. The null hypothesis for this test is that X1 and X2 have the same continuous distribution. The alternative hypothesis is that they have different continuous distributions. The result H is 1 if we can reject the hypothesis that the distributions are the same, or 0 if we cannot reject that hypothesis. We reject the hypothesis if the test is significant at the 5% level.
For each potential value x, the Kolmogorov-Smirnov test compares the proportion of X1 values less than x with proportion of X2 values less than x. The kstest2 function uses the maximum difference over all x values is its test statistic. Mathematically, this can be written as
where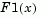 
is the proportion of X1 values less than or equal to x and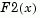 
is the proportion of X2 values less than or equal to x.
H = kstest2(X1,X2,alpha, specifies the significance level tail)
alpha and a code tail for the type of alternative hypothesis. If tail = 0 (the default), kstest performs a two-sided test with the general alternative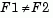 
. If tail = -1, the alternative is that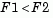 
. If tail = 1, the alternative is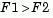 
. The form of the test statistic depends on the value of tail as follows:
tail= 0: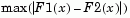
tail= -1: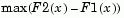
tail= 1: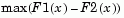
[H,P,KSSTAT,CV] = kstest(X,cdf,alpha,tail)
also returns the observed p-value P, the observed Kolmogorov-Smirnov statistic KSSTAT, and the cutoff value CV for determining if KSSTAT is significant. If the return value of CV is NaN, then kstest determined the significance calculating a p-value according to an asymptotic formula rather than by comparing KSSTAT to a critical value.
Examples
Let's compare the distributions of a small evenly-spaced sample and a larger normal sample:
x = -1:1:5
y = randn(20,1);
[h,p,k] = kstest2(x,y)
h =
1
p =
0.0403
k =
0.5714
The difference between their distributions is significant at the 5% level (p = 4%). To visualize the difference, we can overlay plots of the two empirical cumulative distribution functions. The Kolmogorov-Smirnov statistic is the maximum difference between these functions. After changing the color and line style of one of the two curves, we can see that the maximum difference appears to be near x = 1.9. We can also verify that the difference equals the k value that kstest2 reports:
cdfplot(x)
hold on
cdfplot(y)
h = findobj(gca,'type','line');
set(h(1),'linestyle',':','color','r')
1 - 3/7
ans =
0.5714
See Also
| | kstest | kurtosis | |
