

| Spline Toolbox |   |
Put together a spline in B-form
Syntax
spmak sp = spmak(knots,coefs) sp = spmak(knots,coefs,sizec)
Description
spmak puts together a spline function in B-form, from minimal information, with the rest inferred from the input. fnbrk returns all the parts of the completed description. In this way, the actual data structure used for the storage of this form is easily modified without any effect on the various commands using the construct.
If there are no arguments, you will be prompted for knots and coefs.
The coefficients may be d-vectors (e.g., 2-vectors or 3-vectors), in which case the resulting spline is a curve or surface (in 2-space or 3-space).
The action taken by spmak depends on whether the function is univariate or multivariate, as indicated by knots being a sequence or a cell-array.
If knots is a sequence (required to be non-decreasing), then the spline is taken to be univariate, of order k = length(knots) - size(coefs,2). This means that each column of coefs is taken to be a B-spline coefficient of the spline. This follows the general agreement in this package that, in case of a vector-valued spline, any vector in its target, be it a coefficient, or the value of the spline at a site, is written as a 1-column matrix. In particular, the spline is d-vector-valued, with d = size(coefs,1). Finally, the basic interval of the B-form is [knots(1) .. knots(end)].
Knot multiplicity is held to be 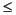
k. This means that the coefficient coefs(:,j) is simply ignored in case the corresponding B-spline has only one distinct knot, i.e., in case knots(j)==knots(j+k).
If knots is a cell array, of length m, then the spline is taken to be m-variate, and coefs must be an (m+1)-dimensional array, - except when the spline is to be scalar-valued, in which case, in contrast to the univariate case, coefs is permitted to be an m-dimensional array, but this array is immediately reshaped by
coefs = reshape(coefs, [1,size(coefs)]);
With this, the ith entry of m-vector k is computed as length(knots{i}) - size(coef,i+1), i=1:m, and the ith entry of the cell array of basic intervals is set to [knots{i}(1), knots{i}(end)].
Since, MATLAB suppresses trailing singleton dimensions, you must use the optional third input argument to supply the desired size of the input array coefs in case it has one or more trailing singleton dimensions.
Examples
spmak([1:6],[0:2]) constructs a spline function with basic interval [1. .6], with 6 knots and 3 coefficients, hence of order 6 - 3 = 3. spmak(t,1) provides the B-spline B(.|t) in ppform. See spalldem for other examples.
If the intent is to construct a 2-vector valued bivariate polynomial on the rectangle 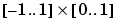 , linear in the first variable and constant in the second, say
, linear in the first variable and constant in the second, say coefs = zeros([2 2 1]); coefs):, :,1) = [1 0;0 1]; then the straightforward
sp = spmak({[-1 -1 1 1],[0 1]},coefs);
will fail, producing a scalar-valued function of (illegal) order [2 0], while proper use of that third argument, as in
sp = spmak({[-1 -1 1 1],[0 1]},coefs,[2 2 1]);
See spalldem for other examples.
See Also
Diagnostics
There will be an error return if the proposed knot sequence fails to be nondecreasing or if there are not more knots than there are coefficients, or if the coefficient array is empty.
Limitations
The size of a multidimensional array created by the statement reshape(1,[1,1,1,...,1]) will be reported as [1 1]. This means that the B-form created by the statement sp = spmak(knots,1), with knots a cell array of length m>2, will not be interpreted correctly, by fnval and other commands, as the tensor-product B-spline for the given knots.
 | splpp, sprpp | Glossary |  |