

| Spline Toolbox |   |
Put together a spline in ppform
Syntax
ppmak ppmak(breaks,coefs) pp = ppmak(breaks,coefs,d)
Description
ppmak puts together a piecewise-polynomial function in ppform, from minimal information, with the rest inferred from the input. fnbrk returns the parts of the completed description. In this way, the actual data structure used for the storage of this form is easily modified without any effect on the various commands using the construct.
If there are no arguments, you will be prompted for breaks and coefs. However, the casual user is not likely to use ppmak explicitly, relying instead on the various spline construction commands in the toolbox to construct splines that satisfy certain conditions.
The action taken by ppmak depends on whether the function is univariate or multivariate, as indicated by breaks being a sequence or a cell-array.
If breaks is a sequence, which must be nondecreasing, with its first entry different from its last, then the function is assumed to be univariate, and the various parts of its ppform are determined as follows:
l of polynomial pieces is determined as l=length(breaks)-1, and the basic interval is, correspondingly, the interval [breaks(1) .. breaks(l+1)].
k and the dimension d of the function's target are inferred as follows:
d is not given explicitly, then coefs(:,i*k+j) is
assumed to contain the jth coefficient of the (i+1)st polynomial piece
(with the first coefficient the highest and the kth coefficient the lowest or
constant coefficient). Thus the dimension d is obtained from [d,kl] =
size(coefs) and the order k of the piecewise-polynomial is obtained as k
= fix(kl/l).
d is explicitly specified, then coefs(i*d+j,:) is assumed to contain the
jth components of the coefficient vector for the (i+1)st polynomial piece.
This corresponds to the format used internally, while the earlier format
seems easier to handle when specifying such a piecewise-polynomial
explicitly. In particular, it is the format in which fnbrk returns the
coefficient array, hence d must be explicitly specified when the input
coefs is the result of a call to fnbrk.
If breaks is a cell array, of length m, then the function is assumed to be m-variate (tensor product), and the various parts of its ppform are determined from the input as follows:
length(breaks{i})-1 as its ith entry and, correspondingly, the m-cell array of its basic intervals has the interval [breaks{i}(1).. breaks{i}(end)] as its ith entry.
d of the function's target and the m-vector k of (coordinate-wise polynomial) orders of its pieces are obtained directly from the size of coefs, and any third input argument is ignored.
coefs is an m-dimensional array, then the function is taken to be
scalar-valued, i.e., d = 1, and the m-vector k is computed as
size(coefs)./l. After that, coefs is reshaped by the command
coefs = reshape(coefs,[1,size(coefs)]).
coefs is an (m+1)-dimensional array, then d is taken to be
size(coefs,1), and the ith entry of k is computed as size(coefs,i+1)/
l(i), i=1:m.
Since, MATLAB suppresses trailing singleton dimensions, you must use the optional third input argument to supply the desired size of the input array coefs in case it has one or more trailing singleton dimensions.
The coefficient array is internally treated as an equivalent array of size [d,l(1),k(1),l(2),k(2),...,l(m),k(m)], with its (:,i(1),r(1),i(2),r(2),...,i(m),r(m)) entry the coefficient of
(x(1)-breaks{1}(i(1)))^(k(1)-r(1))*...*(x(m)-breaks{m}(i(m)))..
^(k(m)-r(m))
in the local polynomial representation of the function on the (hyper)rectangle
[breaks{1}(i(1))..breaks{1}(i(1)+1)]x...x[breaks{m}(i(m))..
breaks{m}(i(m)+1)]
Examples
ppmak([0:2],[1:6]) constructs a piecewise-polynomial function with basic interval [0..2] and consisting of two pieces of order 3, with the sole interior break 1. The resulting function is scalar, i.e., the dimension d of its target is 1. The function happens to be continuous at that break since the first piece is 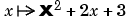 while the second piece is
while the second piece is
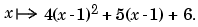
When the function is univariate and the dimension d is not explicitly specified, then it is taken to be the row number of coefs. The column number should be an integer multiple of the number 1 of pieces specified by breaks. For example, the statement ppmak([0:2],[1:3;4:6]) leads to an error, since the break sequence [0:2] indicates two polynomial pieces, hence an even number of columns are expected in the coefficient matrix. The modified statement ppmak([0:1],[1:3;4:6]) specifies the parabolic curve
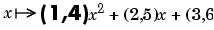 In particular, the dimension
In particular, the dimension d of its target is 2. The differently modified statement ppmak([0:2],[1:4;5:8]) also specifies a planar (i.e., d = 2) curve, but this one is piecewise linear; its first polynomial piece is 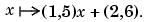
Explicit specification of the dimension d leads, in the univariate case, to a different interpretation of the entries of coefs. Now the column number indicates the polynomial order of the pieces, and the row number should equal d times the number of pieces. Thus, the statement ppmak([0:2],[1:4;5:8],2) is in error, while the statement ppmak([0:2],[1:4;5:8],1) specifies a scalar piecewise cubic whose first piece is 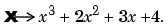
See ppalldem for other examples.
See Also
fnbrk, ppalldem
 | optknt | rpmak, rsmak |  |