

| Spline Toolbox |   |
Directional derivative of a function
Syntax
df = fndir(f,direction)
Description
Let f be the function described by f, let y be the sole column of the matrix direction, and assume that y has as many entries as the function f has arguments. Then df is the ppform of the directional derivative of f in the direction y, i.e., of the function
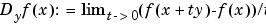 .
.
If the matrix direction has n columns and f is m-valued, then the function in df is (mn)-valued. Its value at x, reshaped as a matrix of size (m,n), has in its jth column the directional derivative of f at x in the direction of the jth column of direction.
Examples
For example, if f describes a d-variate m-vector-valued function and x is some point in its domain, then
reshape(fnval(fndir(f,eye(d)),x),m,d)
is the Jacobian of that function at that point.
As a related example, the next statements plot the gradients of (a good approximation to) the Franke function at a regular mesh:
xx = linspace(-.1,1.1,13); yy = linspace(0,1,11);
[x,y] = ndgrid(xx,yy); z = franke(x,y);
pp2dir = fndir(csapi({xx,yy},z),eye(2));
grads = reshape(fnval(pp2dir,[x(:) y(:)].'),...
[2,length(xx),length(yy)]);
quiver(x,y,squeeze(grads(1,:,:)),squeeze(grads(2,:,:)))
Algorithm
The function in f is converted to ppform, and the directional derivative of its polynomial pieces is computed formally and in one vector operation, and put together again to form the ppform of the directional derivative of the function in f.
See Also
 | fnder | fnint |  |