| Spline Toolbox | |
Syntax
fn = fncmb(function,matrix) fn = fncmb(function,function) fn = fncmb(function,matrix,function) fn = fncmb(function,matrix,function,matrix) fn = fncmb(function,'op',function)
Description
The intent is to make it easy to carry out the standard linear operations of scaling and adding within a spline space. More than that, a matrix may be applied to a vector-valued function, and even two (univariate) functions in different forms may be added or multiplied pointwise.
Examples
fncmb(fn,3.5) multiplies (the coefficients of) the function in fn by 3.5, while fncmb(f,g) returns the sum of the function in f and in g, and fncmb(f,3,g,-4) returns the linear combination, with weights 3 and -4, of the function in f and the function in g. Also, fncmb(f,3,g) adds 3 times the function in f to the function in g.
Assuming, more generally, that the function f in f is d-vector-valued for some d, and that, correspondingly, A is a matrix of size [r,d] for some r, then the statement fncmb(f,A) returns the description of the function
As a simple example, if the function f in f happens to be scalar-valued, then f3=fncmb(f,[1;2;3]) contains the description of the function whose value at x is the 3-vector (f(x),2f(x),3f(x)). Note that, by the convention throughout this toolbox, the subsequent statement fnval(f3, x) returns a 1-column-matrix. As another simple example, if f describes a surface in 3-space, i.e., the function in f is 3-vector-valued bivariate, then f2 = fncmb(f,[1 0 0;0 0 1]); describes the projection of that surface to the (x,z)-plane. As another example, if t is a knot sequence of length n+k and a is a matrix with n columns, then fncmb(spmak(t,eye(n,n)),a) is the same as spmak(t,a).
Finally, fncmb(spmak([0:4],1),'+',ppmak([-1 5],[1 -1])) is the piecewise-polynomial with breaks -1:5 that, on the interval [0 .. 4], agrees with the function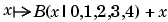 
(but has no active break at 0 or 1, hence differs from this function outside the interval [0 .. 4]), while fncmb(spmak([0:4],1),'-',0) has the same effect as fn2fm(spmak([0:4],1),'pp').
Algorithm
The coefficients are extracted (via fnbrk) and operated on by the specified matrix (and, possibly, added), then recombined with the rest of the function description (via ppmak or spmak). If there are two functions input, then they must be of the same type (see Limitations, below) except for the following:
fncmb(f1,'op',f2) returns the ppform of the function
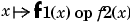
with op one of +, -, *, and f1, f2 of arbitrary form. In addition, if f2 is a scalar, it is taken to be the function that is constantly equal to that scalar.
Limitations
fncmb only works for univariate functions, except for the case when there is just one function in the input.
Further, if two functions are involved, then they must be of the same type. This means that they must either both be in B-form or both be in ppform, and, moreover, have the same knots or breaks, the same order, and the same target. The only exception to this is the command of the form fncmb(function,'op',function).
Cautionary Note
This matching condition is not checked for explicitly. But, MATLAB will issue an error message about incompatible sizes if the two coefficient arrays involved do not agree in size.
| | fnbrk | fnder | |
