Transfer Fcn (Using Simulink)

Implement a linear transfer function.

Library

Continuous

Description

The Transfer Fcn block implements a transfer function where the input (u) and output (y) can be expressed in transfer function form as the following equation

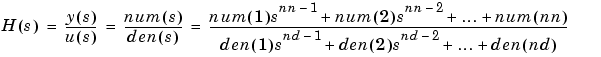
where nn and nd are the number of numerator and denominator coefficients, respectively. num and den contain the coefficients of the numerator and denominator in descending powers of s. num can be a vector or matrix, den must be a vector, and both are specified as parameters on the block dialog box. The order of the denominator must be greater than or equal to the order of the numerator.

A Transfer Fcn block takes a scalar input. If the numerator of the block's transfer function is a vector, the block's output is also scalar. However, if the numerator is a matrix, the transfer function expands the input into an output vector equal in width to the number of rows in the numerator. For example, a two-row numerator results in a block with scalar input and vector output. The width of the output vector is two.

Initial conditions are preset to zero. If you need to specify initial conditions, convert to state-space form using tf2ss and use the State-Space block. The tf2ss utility provides the A, B, C, and D matrices for the system. For more information, type help tf2ss or consult the Control System Toolbox documentation.

The Transfer Fcn Block Icon

The numerator and denominator are displayed on the Transfer Fcn block icon depending on how they are specified:

If each is specified as an expression, a vector, or a variable enclosed in parentheses, the icon shows the transfer function with the specified coefficients and powers of s. If you specify a variable in parentheses, the variable is evaluated. For example, if you specify Numerator as [3,2,1] and Denominator as (den) where den is [7,5,3,1], the block icon looks like this: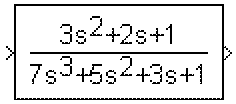

If each is specified as a variable, the icon shows the variable name followed by "(s)". For example, if you specify Numerator as num and Denominator as den, the block icon looks like this:

Data Type Support

A Transfer Fcn block accepts and outputs signals of type double.

Parameters and Dialog Box

Numerator: The row vector of numerator coefficients. A matrix with multiple rows can be specified to generate multiple output. The default is [1].
Denominator: The row vector of denominator coefficients. The default is [1 1].

Characteristics

Direct Feedthrough
Only if the lengths of the Numerator and Denominator parameters are equal

Sample Time
Continuous

Scalar Expansion
No

States
Length of Denominator -1

Dimensionalized
Yes, in the sense that the block expands scalar input into vector output when the transfer function numerator is a matrix. See block description above.

Zero Crossing
No

Direct Feedthrough	Only if the lengths of the Numerator and Denominator parameters are equal
Sample Time	Continuous
Scalar Expansion	No
States	Length of Denominator -1
Dimensionalized	Yes, in the sense that the block expands scalar input into vector output when the transfer function numerator is a matrix. See block description above.
Zero Crossing	No

To Workspace Transport Delay