remez (Signal Processing Toolbox)

Compute the Parks-McClellan optimal FIR filter design.

Syntax

b = remez(n,f,a)
b = remez(n,f,a,w)
b = remez(n,f,a,'ftype')
b = remez(n,f,a,w,'ftype')
b = remez(...,{lgrid})
b = remez(n,f,'fresp',w)
b = remez(n,f,'fresp',w,'ftype')
b = remez(n,f,{'fresp',p1,p2,...},w)
b = remez(n,f,{'fresp',p1,p2,...},w,'ftype')
[b,delta] = remez(...)
[b,delta,opt] = remez(...)

Description

remez designs a linear-phase FIR filter using the Parks-McClellan algorithm [1]. The Parks-McClellan algorithm uses the Remez exchange algorithm and Chebyshev approximation theory to design filters with an optimal fit between the desired and actual frequency responses. The filters are optimal in the sense that the maximum error between the desired frequency response and the actual frequency response is minimized. Filters designed this way exhibit an equiripple behavior in their frequency responses and are sometimes called equiripple filters.

b = remez(n,f,a) returns row vector b containing the n+1 coefficients of the order n FIR filter whose frequency-amplitude characteristics match those given by vectors f and a.

The output filter coefficients (taps) in b obey the symmetry relation

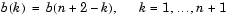
Vectors f and a specify the frequency-magnitude characteristics of the filter:

f is a vector of pairs of normalized frequency points, specified in the range between 0 and 1, where 1 corresponds to the Nyquist frequency. The frequencies must be in increasing order.

a is a vector containing the desired amplitudes at the points specified in f.

The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k odd is the line segment connecting the points (f(k), a(k)) and (f(k+1), a(k+1)).

The desired amplitude at frequencies between pairs of points (f(k), f(k+1)) for k even is unspecified. The areas between such points are transition or "don't care" regions.

f and a must be the same length. The length must be an even number.

The relationship between the f and a vectors in defining a desired frequency response is shown in the example below.

remez always uses an even filter order for configurations with a passband at the Nyquist frequency. This is because for odd orders, the frequency response at the Nyquist frequency is necessarily 0. If you specify an odd-valued n, remez increments it by 1.

remez(n,f,a,w) uses the weights in vector w to weight the fit in each frequency band. The length of w is half the length of f and a, so there is exactly one weight per band.

b = remez(n,f,a,'ftype') and

b = remez(n,f,a,w,'ftype') specify a filter type, where 'ftype' is

'hilbert', for linear-phase filters with odd symmetry (type III and type IV)

The output coefficients in b obey the relation b(k) = -b(n+2-k), k = 1, ..., n + 1. This class of filters includes the Hilbert transformer, which has a desired amplitude of 1 across the entire band.

For example,

h = remez(30,[0.1 0.9],[1 1],'hilbert');

designs an approximate FIR Hilbert transformer of length 31.

'differentiator', for type III and type IV filters, using a special weighting technique

For nonzero amplitude bands, it weights the error by a factor of 1/f so that the error at low frequencies is much smaller than at high frequencies. For FIR differentiators, which have an amplitude characteristic proportional to frequency, these filters minimize the maximum relative error (the maximum of the ratio of the error to the desired amplitude).

b = remez(...,{lgrid}) uses the integer lgrid to control the density of the frequency grid, which has roughly (lgrid*n)/(2*bw) frequency points, where bw is the fraction of the total frequency band interval [0,1] covered by f. Increasing lgrid often results in filters that more exactly match an equiripple filter, but that take longer to compute. The default value of 16 is the minimum value that should be specified for lgrid. Note that the {lgrid} argument must be a 1-by-1 cell array.

b = remez(n,f,'fresp',w) returns row vector b containing the n+1 coefficients of the order n FIR filter whose frequency-amplitude characteristics best approximate the response specified by function fresp. The function is called from within remez with the following syntax.

[dh,dw] = fresp(n,f,gf,w)

The arguments are similar to those for remez:

n is the filter order.

f is the vector of normalized frequency band edges that appear monotonically between 0 and 1, where 1 is the Nyquist frequency.

gf is a vector of grid points that have been linearly interpolated over each specified frequency band by remez. gf determines the frequency grid at which the response function must be evaluated, and contains the same data returned by cremez in the fgrid field of the opt structure.

w is a vector of real, positive weights, one per band, used during optimization. w is optional in the call to remez; if not specified, it is set to unity weighting before being passed to fresp.

dh and dw are the desired complex frequency response and band weight vectors, respectively, evaluated at each frequency in grid gf.

The predefined frequency response function fresp that remez calls is remezfrf in the signal/private directory.

b = remez(n,f,{'fresp',p1,p2,...},w) allows you to specify additional parameters (p1, p2, etc.) to pass to fresp. Note that b = remez(n,f,a,w) is a synonym for b = remez(n,f,{'remezfrf',a},w), where a is a vector containing the desired amplitudes at the points specified in f.

b = remez(n,f,'fresp',w,'ftype') and

b = remez(n,f,{'fresp',p1,p2,...},w,'ftype') design antisymmetric (odd) rather than symmetric (even) filters, where 'ftype' is either 'd' for a differentiator or 'h' for a Hilbert transformer.

In the absence of a specification for ftype, a preliminary call is made to fresp to determine the default symmetry property sym. This call is made using the syntax.

sym = fresp('defaults',{n,f,[],w,p1,p2,...})

The arguments n, f, w, etc., may be used as necessary in determining an appropriate value for sym, which remez expects to be either 'even' or 'odd'. If the fresp function does not support this calling syntax, remez defaults to even symmetry.

[b,delta] = remez(...) returns the maximum ripple height in delta.

[b,delta,opt] = remez(...) returns a structure with the following fields.

opt.fgrid
Frequency grid vector used for the filter design optimization

opt.des
Desired frequency response for each point in opt.fgrid

opt.wt
Weighting for each point in opt.fgrid

opt.H
Actual frequency response for each point in opt.fgrid

opt.error
Error at each point in opt.fgrid (opt.des-opt.H)

opt.iextr
Vector of indices into opt.fgrid for extremal frequencies

opt.fextr
Vector of extremal frequencies

`opt.fgrid`	Frequency grid vector used for the filter design optimization
`opt.des`	Desired frequency response for each point in `opt.fgrid`
`opt.wt`	Weighting for each point in `opt.fgrid`
`opt.H`	Actual frequency response for each point in `opt.fgrid`
`opt.error`	Error at each point in `opt.fgrid` (`opt.des-opt.H`)
`opt.iextr`	Vector of indices into `opt.fgrid` for extremal frequencies
`opt.fextr`	Vector of extremal frequencies

Example

Graph the desired and actual frequency responses of a 17th-order Parks-McClellan bandpass filter.

f = [0 0.3 0.4 0.6 0.7 1]; a = [0 0 1 1 0 0];
b = remez(17,f,a);
[h,w] = freqz(b,1,512);
plot(f,a,w/pi,abs(h))
legend('Ideal','remez Design')

Algorithm

remez is a MEX-file version of the original Fortran code from [1], altered to design arbitrarily long filters with arbitrarily many linear bands.

remez designs type I, II, III, and IV linear-phase filters. Type I and type II are the defaults for n even and n odd, respectively, while type III (n even) and type IV (n odd) are obtained with the 'hilbert' and 'differentiator' flags. The different types of filters have different symmetries and certain constraints on their frequency responses (see [5] for more details).

Linear Phase Filter Type
Filter Order
Symmetry of Coefficients
Response H(f), f = 0
Response H(f), f = 1 (Nyquist)

Type I
Even
even:

No restriction
No restriction

Type II
Odd
No restriction
H(1) = 0

Type III
Even
odd:

H(0) = 0
H(1) = 0

Type IV
Odd
H(0) = 0
No restriction

Linear Phase Filter Type	Filter Order	Symmetry of Coefficients	Response H(f), f `=` 0	Response H(f), f `=` 1 (Nyquist)
Type I	Even	even:	No restriction	No restriction
Type II	Odd	No restriction	H(1) `=` 0
Type III	Even	odd:	H(0) `=` 0	H(1) `=` 0
Type IV	Odd	H(0) `=` 0	No restriction

Remarks

If you get the following warning message,

-- Failure to Converge --
Probable cause is machine rounding error.

it is possible that the filter design may still be correct. Verify the design by checking its frequency response.

See Also

butter
Design a Butterworth analog and digital filter .

cheby1
Design a Chebyshev type I filter (passband ripple).

cheby2
Design a Chebyshev type II filter (stopband ripple).

cremez
Design a complex and nonlinear-phase equiripple FIR filter.

ellip
Design an elliptic (Cauer) filter.

fir1
Design a window-based finite impulse response filter: standard response.

fir2
Design a window-based finite impulse response filter: arbitrary response.

fircls
Design a constrained least square FIR filter for multiband filters.

fircls1
Design a constrained least square filter for lowpass and highpass linear phase FIR filters.

firls
Design a least square linear-phase FIR filter.

firrcos
Design a raised cosine FIR filter.

gremez
Design a generalized Remez optimal FIR filter design (see the Filter Design Toolbox documentation).

remezord
Estimate the Parks-McClellan optimal FIR filter order.

yulewalk
Design a recursive digital filter.

`butter`	Design a Butterworth analog and digital filter .
`cheby1`	Design a Chebyshev type I filter (passband ripple).
`cheby2`	Design a Chebyshev type II filter (stopband ripple).
`cremez`	Design a complex and nonlinear-phase equiripple FIR filter.
`ellip`	Design an elliptic (Cauer) filter.
`fir1`	Design a window-based finite impulse response filter: standard response.
`fir2`	Design a window-based finite impulse response filter: arbitrary response.
`fircls`	Design a constrained least square FIR filter for multiband filters.
`fircls1`	Design a constrained least square filter for lowpass and highpass linear phase FIR filters.
`firls`	Design a least square linear-phase FIR filter.
`firrcos`	Design a raised cosine FIR filter.
`gremez`	Design a generalized Remez optimal FIR filter design (see the Filter Design Toolbox documentation).
`remezord`	Estimate the Parks-McClellan optimal FIR filter order.
`yulewalk`	Design a recursive digital filter.

References

[1] Programs for Digital Signal Processing, IEEE Press, New York, 1979, Algorithm 5.1.

[2] Selected Papers in Digital Signal Processing, II, IEEE Press, New York, 1979.

[3] Parks, T.W., and C.S. Burrus, Digital Filter Design, John Wiley & Sons, New York:, 1987, p. 83.

[4] Rabiner, L.R., J.H. McClellan, and T.W. Parks, "FIR Digital Filter Design Techniques Using Weighted Chebyshev Approximations," Proc. IEEE 63 (1975).

[5] Oppenheim, A.V., and R.W. Schafer, Discrete-Time Signal Processing, Prentice-Hall, Englewood Cliffs, NJ, 1989, pp. 256-266.

rectpuls remezord