

| Signal Processing Toolbox |   |
Generalized digital Butterworth filter design.
Syntax
[b,a,]=maxflat(nb,na,Wn) b=maxflat(nb,'sym',Wn) [b,a,b1,b2]=maxflat(nb,na,Wn) [...]=maxflat(nb,na,Wn,'design_flag')
Description
[b,a,] is a lowpass Butterworth filter with numerator and denominator coefficients = maxflat(nb,na,Wn)
b and a of orders nb and na respectively. Wn is the normalized cutoff frequency at which the magnitude response of the filter is equal to 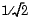 (approx. -3 dB).
(approx. -3 dB). Wn must be between 0 and 1, where 1 corresponds to the Nyquist frequency.
b is a symmetric FIR Butterworth filter. = maxflat(nb,'sym',Wn)
nb must be even, and Wn is restricted to a subinterval of [0,1]. The function raises an error if Wn is specified outside of this subinterval.
[b,a,b1,b2] returns two polynomials = maxflat(nb,na,Wn)
b1 and b2 whose product is equal to the numerator polynomial b (that is, b = conv(b1,b2)). b1 contains all the zeros at z = -1, and b2 contains all the other zeros.
[...] enables you to monitor the filter design, where = maxflat(nb,na,Wn,'design_flag')
'design_flag' is:
'trace', for a textual display of the design table used in the design'plots', for plots of the filter's magnitude, group delay, and zeros and poles'both', for both the textual display and plotsExamples
nb=10; na=2; Wn=0.2; [b,a,b1,b2]=maxflat(nb,na,Wn,'plots')
Algorithm
The method consists of the use of formulae, polynomial root finding, and a transformation of polynomial roots.
See Also
|
Butterworth analog and digital filter design. |
|
Filter data with a recursive (IIR) or nonrecursive (FIR) filter. |
|
Compute the frequency response of digital filters. |
References
[1] Selesnick, I.W., and C.S. Burrus, "Generalized Digital Butterworth Filter Design," Proceedings of the IEEE Int. Conf. Acoust., Speech, Signal Processing, Vol. 3 (May 1996).
 | lsf2poly | medfilt1 |  |