

| Robust Control Toolbox |   |
Compute an upper bound on the structured singular value via the Perron eigenvector method.
[mu] = perron(a) [mu] = perron(a,k) [mu,ascaled,logd] = psv(a) [mu,ascaled,logd] = psv(a,k)
Description
perron produces the Perron eigenvalue for a given real or complex p by q matrix. This value serves as a scalar upper bound "mu" on the Structured Singular Value (SSV).
psv computes a tighter SSV upper bound mu via the formula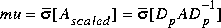 where Dp = diag(exp(logd)) is the Perron optimal diagonal scaling. In addition,
where Dp = diag(exp(logd)) is the Perron optimal diagonal scaling. In addition, psv returns the log magnitude of the optimal diagonal scaling logd in a column vector, and the scaled matrix 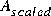 is returned in
is returned in ascaled.
The optional input k records the uncertainty block sizes with default valuek can be an n by 1 or
Algorithm
The values of mu and logd are found by examining the eigenvalues and eigenvectors of the n by n nonnegative square matrix F formed from by A replacing each block of A (as defined by the partitioning k) by its greatest singular value. For any given positive square matrix (i.e., matrix with positive entries), there exists a positive real eigenvalue 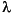 p of multiplicity one whose magnitude is greater than the real part of any other eigenvalue,
p of multiplicity one whose magnitude is greater than the real part of any other eigenvalue,
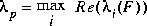 :
:
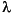 p is called the Perron eigenvalue of F, and its left and right eigenvectors, denoted as yp and xp respectively, are called Perron eigenvectors.
In 1982, Safonov [1] showed that the Perron eigenvalue is a good upper bound on the structured singular value µ, i.e.,
p is called the Perron eigenvalue of F, and its left and right eigenvectors, denoted as yp and xp respectively, are called Perron eigenvectors.
In 1982, Safonov [1] showed that the Perron eigenvalue is a good upper bound on the structured singular value µ, i.e.,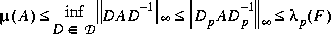
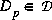 is the Perron optimal scaling matrix
is the Perron optimal scaling matrix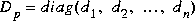 and
and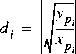 Moreover, the above inequalities become equalities when A = F so that, in the case in which A is a positive matrix and the uncertainty blocks are scalar, the Perron eigenvalue bound on µ is tight.
For reducible matrices the Perron optimal scaling matrix Dp can be singular, which would lead to numerical instability if corrective action were not taken. This problem is solved in
Moreover, the above inequalities become equalities when A = F so that, in the case in which A is a positive matrix and the uncertainty blocks are scalar, the Perron eigenvalue bound on µ is tight.
For reducible matrices the Perron optimal scaling matrix Dp can be singular, which would lead to numerical instability if corrective action were not taken. This problem is solved in psv (in the same fashion as it is in the function osborne) by very slightly perturbing the matrix F to a nearby irreducible matrix which has a slightly greater Perron eigenvalue. See osborne for further details and examples. Perturbation is not required with the perron function since Dp is not computed.
As compared to Osborne or nonlinear programming techniques, Perron eigenvector algorithms implemented by perron and psv require no iteration and so tend to be faster.
Examples
Several problems can be solved via the following psv commands, where most careless algorithms fail:
% An reducible case as compared to sigma A = eye(10); A(1,10) = 100000; [mu,Ascaled,logd] = psv(A); s1 = max(svd(A)); [s1, mu], % Another reducible case as compared to sigma A = eye(8); A(1,3) = 100000; A(4,8) = 500000; [mu,Ascaled,logd] = psv(A); s1 = max(svd(A)); [s1, mu],
See Also
muopt, osborne, ssv, sigma, dsigma
References
[1] M. G. Safonov, "Stability Margins for Diagonally Perturbed Multivariable Feedback Systems," IEE Proc., vol. 129, Part D, pp. 251-256, 1982.
 | osborne | reig |  |