| Robust Control Toolbox | |
Optimal Hankel minimum degree approximation without balancing.
[ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,Type) [ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,Type,in) [am,bm,cm,dm,totbnd,svh] = ohklmr(a,b,c,d,Type) [am,bm,cm,dm,totbnd,svh] = ohklmr(a,b,c,d,Type,in) [ssx,ssy,] = ohkapp(ss,) [ssm,] = ohklmr(ss,..)
Description
ohkapp computes the kth order optimal Hankel minimum degree approximation (OHMDA)
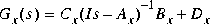
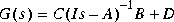such that Gx is stable and
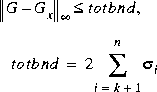where 
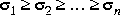denote Hankel singular values of G(s), i.e., the square roots of eigenvalues of PQ, where P and Q are the reachability and observability grammians of (A, B, C, D).
An anticausal Gy(s) is also returned in (Ay, By, Cy, Dy). Together Gx(s) and Gy(s) possess the following important property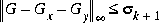
[ax,bx,cx,dx,ay,by,cy,dy,aug] = ohkapp(a,b,c,d,1,0) computes the zeroth order OHMDA, i.e., the anticausal OHMDA of a stable system, which is an important intermediate step of the L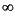
control synthesis.
Variable aug contains the following information:
aug(1,1) =1 aug(1,2) = number of states removed aug(1,3) = totbnd aug(4:4+n-1) = [
ohklmr also computes the kth order OHMDA, but allows the system to be unstable. It works by applying ohkapp to the stable and antistable parts of G(s) (obtained via stabproj), then applying addss. Totbnd returns the L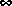
norm error bound of the approximation. Variable svh returns the Hankel singular values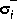 
of [G(s)]- (stable part) and 
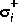of [G(-s)]+ (reversed antistable part), i.e.,
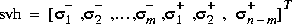where m denotes the number of stable roots, n- m denotes the number of unstable roots.
Both ohkapp and ohklmr provide three options:
ype = 1, in = k, size of reduced order model.
Type = 2, in = tol, find a kth order reduced model such that the total error totbnd
is less than tol.
Type = 3, display svh and prompt for k + 1. In this case, there is no need to
assign a value for in.
Algorithm
ohkapp and ohklmr employ the algorithm described in [3], which is a "basis-free" descriptor system implementation of the OHMDA. The descriptor formulae bypass the numerically ill-conditioned balanced realization step required by the earlier state-space formulae [1, 2].
ohklmr uses the M-function stabproj to split G(s) into the sum of stable and antistable parts, then applies ohkapp to each part.
See Also
balmr, mrdemo, obalreal, bstschmr, schmr, stabproj
References
[1] M. Bettayeb, L. M. Silverman and M. G. Safonov, "Optimal Approximation of Continuous Time Systems," IEEE Conf. on Decision and Control, Albuquerque, NM, Dec. 10-12, 1981.
-error Bounds," Int. J. Control, vol. 39, no. 6, pp. 1145-1193, 1984.
[3] M. G. Safonov, R. Y. Chiang, and D. J. N. Limebeer, "Hankel Model Reduction without Balancing -- A Descriptor Approach," Proc. IEEE Conf. on Decision and Control, Los Angeles, CA, Dec. 9-11, 1987, also "Optimal Hankel Model Reduction for Nonminimal Systems," IEEE Trans. on Automat. Contr., vol. 34, no. 4, pp. 496-502, 1990.
| obalreal | osborne | |