musyn (Robust Control Toolbox)

µ synthesis procedure.

[acp,,dcp,mu,logd,ad,,dd,gam] = musyn(A,B1,B2,,D22,w) 
[acp,,dcp,mu,logd,ad,,dd,gam] = ...
     musyn(A,B1,B2,,D22,w,gammaind,aux,logd0,n,blksz,flag)
[sscp,mu,logd,ssd,gam] = musyn(tss,w) 
[sscp,mu,logd,ssd,gam] = ...
     musyn(tss,w,gammaind,aux,logd0,n,blksz,flag)

Description
Given a two-port plant state space (in its regular form mksys data form tss):

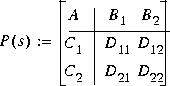
musyn automates the µ synthesis D - F iteration procedure that iteratively applies hinfopt and fitd to find a control law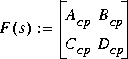

and a diagonal scaling matrix

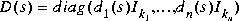that attempts to satisfy the robust performance objective

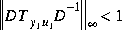Here the identity matrices

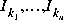are of dimensions determined by the input variable blksz described below.

The resulting structured singular value upper bound µ is returned together with the control law F(s) (sscp). The variable logd returns as its rows the log magnitude frequency response of the diagonal entries of the diagonal scaling matrix D(s).

Also returned is a state-space realization of the D(s) used in the hinfopt portion of the last D - F iteration along with the corresponding optimal value of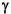

(gam) from the hinfopt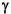

-iteration. See the documentation of hinfopt for further details.

The input variable w contains the frequency at which the structured singular value µ is to be evaluated. The remaining input variables gammaind, aux, logd0, n, blksz, and flag are optional. The variable logd0 allows you to specify an initial guess for logd (default D(s) = I). See the documentation for fitd for an explanation of n, blksz, and flag and their default values. The documentation for hinfopt explains the uses and defaults for the optional input variables gammaind and aux. If an optional variable is given as the empty matrix [ ], then it assumes its default value.

Examples
Following are the MATLAB input commands for a simple µ-synthesis problem:

% PLANT DATA:
a=2;         b1=[.1,-1];         b2=-1; 
c1=[1;.01];  d11=[.1,.2;.01,.01];d12=[1; 0]; 
c2=1;        d21=[0,1];          d22=3; 

tss=mksys(a,b1,b2,c1,c2,d11,d12,d21,d22,'tss');
w = logspace(-2,1); % FREQUENCY VECTOR

% Starting µ Synthesis D-F Iterations: 
[sscp,mu,logd0] = musyn(tss,w);

% DISPLAY OPTIMAL MU PLOTS: 
loglog(w,mu);

% Now improve using frequency dependent D(s): 
[sscp,mu1,logd1] = musyn(tss,w,[ ],[ ],logd0,1);

% DISPLAY OPTIMAL MU PLOTS: 
loglog(w,mu,w,mu1);

The foregoing example illustrates the basic µ-synthesis iteration. In practice, you will generally prefer to use a constant (n = 0) diagonal scaling matrix D(s) because it leads to a much lower order control law. It may also be necessary to experiment with the frequency range w, adjusting it so that it coincides roughly with the frequency range over which the value of µ returned by ssv is unacceptably large. In "Design Case Studies" of the Tutorial a more detailed µ-synthesis example is provided.

Algorithm
The D - F iteration procedure is as follows [1, 2]:

Initialize: If the input variable logd0 is present, go to Step 3; otherwise set D(s) = I and continue.

1: Use the H control method (hinf) to find an F(s) which minimizes the cost

: function .

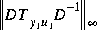2: Use ssv to estimate the structured singular value Bode plot and the corresponding frequency response of logd. The function ssv computes an upper bound on the structured singular value µ and produces the corresponding D(s) by attempting, at each frequency 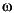, to solve the minimization .

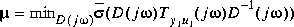3: If the cost is small enough stop; otherwise continue.

4: Using fitd, curve fit an order n rational approximation to each of the diagonal elements of the D(s) obtained in Step 2 and, using augd, augment the plant tsswith the fitted D(s). Go to Step 1.

See the Tutorial chapter "Design Case Studies" for further discussion.

The order of the µ-synthesis controller can be large when a frequency dependent D(s) is employed. The order in general is equal to the order of the plant plus twice the order of D(s). For example, if the plant tss has six states and D(s) has six states, then the order of the µ-synthesis control law will be18, i.e., three times the order of the original plant. This highly limits the potential of practical applications and hardware implementations. Therefore, it is desirable to use as low an order D(s) as is possible; preferably a constant D(s). The combined D - F iteration procedure is not convex, so in general the µ synthesis controller resulting from the D - F iteration is suboptimal.

See Also
hinf, augd, fitd, fitgain, ssv

References
[1] M. G. Safonov, "L Optimization vs. Stability Margin," Proc. IEEE Conf. on Decision and Control, San Antonio, TX, December 14-16, 1983.

[2] J. C. Doyle, "Synthesis of Robust Controllers and Filters," Proc. IEEE Conf. on Decision and Control, San Antonio, TX, December 14-16, 1983.

muopt normhinf, normh2