

| Robust Control Toolbox |   |
Inner-outer factorization (row type).
Inner-outer factorization (column type).[ain,,ainp,,aout,] = iofr(c)(a,bcd) [ssin,ssinp,ssout] = iofr(c)(ss)
Description
A square transfer function M(s) is outer if it is proper and stable and has an inverse that is also proper and stable. A transfer function 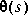 of dimension
of dimension
m by n is inner if it is stable and satisfies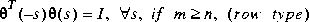
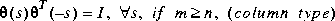 When
When 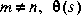 has a complementary inner (or all-pass extension)
has a complementary inner (or all-pass extension) 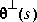
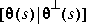 or
or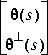 is square and inner.
is square and inner.Iofr computes an inner-outer factorization for a stable transfer function 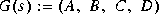 for which m
for which m 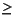 n such that
n such that 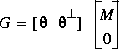 The output variables are defined as
The output variables are defined as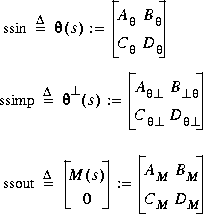
iofc computes an inner-outer factorization for the case of m < n via duality by applying iofr to GT(s), then transposing the result.
Algorithm
iofr implements the algorithm described in [1], where it is shown that inner-outer factorization relates closely to the standard optimal LQ control problem as follows:
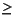 n), the LQR optimal control u = -Fx = -R-1(XB + N)Tx stabilizes the system and minimizes the quadratic cost function
n), the LQR optimal control u = -Fx = -R-1(XB + N)Tx stabilizes the system and minimizes the quadratic cost function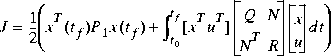 as
as  , satisfies the algebraic Riccati equation
, satisfies the algebraic Riccati equation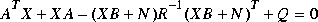 Moreover, the optimal return difference I + L(s) = I + F(Is - A) -1B satisfies the optimal LQ return difference equality:
Moreover, the optimal return difference I + L(s) = I + F(Is - A) -1B satisfies the optimal LQ return difference equality: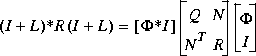 It may be easily shown [1] that the return difference equality implies that an inner-outer factorization of G(s) is given by
It may be easily shown [1] that the return difference equality implies that an inner-outer factorization of G(s) is given by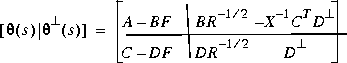 and
and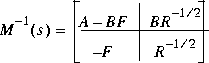 The variables X and F are computed via the MATLAB command:
The variables X and F are computed via the MATLAB command:
[F,X] = lqr(A,B,Q,R,N) = lqr(A,B,C'*C,D'*D,C'*D).The matrix X-1 is a generalized inverse (e.g., a pseudoinverse). Although X may be singular,
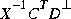 is well defined since the left null-space of
is well defined since the left null-space of 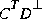 includes the left null-space of X [1].
includes the left null-space of X [1].
Iofc applies iofr to GT(s), then transposes the result.
Limitations
The inner-outer factorization requires the system G(s) to be stable and to have neither poles nor transmission zeros on the j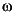 -axis or at
-axis or at 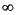 . In particular D must have full column rank for
. In particular D must have full column rank for iofr or full row rank for iofc.
References
[1] J. Doyle, Advances in Multivariable Control. Lecture Notes at ONR/Honeywell Workshop. Minneapolis, MN, Oct. 8-10, 1984.
 | interc | lftf |  |