bstschml, bstschmr (Robust Control Toolbox)

Relative error model reduction via Schur balanced stochastic truncation.

[ared,bred,cred,dred,aug,svh] = bstschmr(A,B,C,D,Type)
[ared,bred,cred,dred,aug,svh] = bstschmr(A,B,C,D,Type,no)
[ared,bred,cred,dred,aug,svh] = bstschmr(A,B,C,D,Type,no,info)
[ssred,aug,svh] = bstschmr(SS,Type) 
[ssred,aug,svh] = bstschmr(SS,Type,no) 
[ssred,aug,svh] = bstschmr(SS,Type,no,info)

The same syntax applies to "bstschml"

Description
Given an nth order stable plant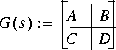

bstschmr computes a kth order reduced model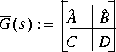

such that the multiplicative error between G(s) and

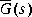is bounded as follows [9]

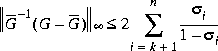and the relative error of G(s) and

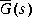also enjoys the same error bound [6]:

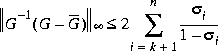where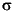

i are the Hankel singular values of the all-pass phase matrix (W*(s))^-1G(s), and

is a minimum phase left spectral factor of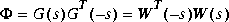

Three options are provided:

1: Type = 1, no = k, size of reduced order model.

2: Type = 2, no = tol, a relative tolerance band in db such that the kth order reduced model 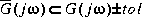for all frequencies.

3: Type = 3, display svh and prompt for k. In this case, no need to assign a value for no.

Variable aug(1,1) returns the number of states that have been removed, while aug(1,2) returns the relative error bound.

Bstschml solves the "dual" problem of bstschmr with the same error bound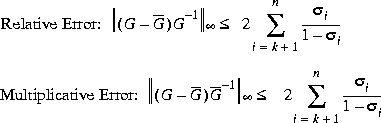

For a given discrete G(z), you can still apply the functions bstschmr and bstschml via bilinear transform bilin to get a reduced order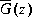

[8], i.e.,

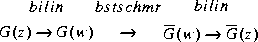The resultant reduced order model

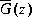enjoys the same relative and multiplicative error bound as the continuous case [7, 9]. A direct discrete BST/REM algorithm without using the bilinear transform is not available at this time.

Algorithm
bstschmr implements the BST model reduction algorithm of [1], but using the Schur method of [4] to bypass the numerical sensitive balancing step. The BST relative error bound is due to Wang and Safonov [6, 9]. The complete algorithm of bstschml and bstschmr is presented in [5].

bstschmr computes the reachability grammian P of G(s) and the observability grammian Q of W(s) via the equations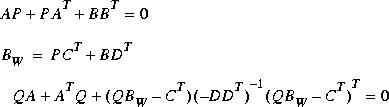

A Schur algorithm, analogous to that in [4], is then applied to the product of the grammians PQ to reliably compute the BST reduced model

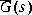. Note that the particular realization of

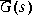, viz. (Ared, Bred, Cred, Dred), will not in general be stochastically balanced.

The BST model reduction procedure produces similar relative error bounds and is closely related to the optimal Hankel norm phase matching model results of [2] and [3].

Bstschml is completely analogous and simply applies the "dual" BST/REM theory. It can also be called by bstschmr with an additional input variable info= "left".

Limitations
The BST model reduction theory requires that D be full rank, for otherwise the Riccati solver fails. For any problem with strictly proper plant, you can shift the j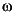-axis via bilin such that BST/REM approximation can be achieved up to a particular frequency range of interest. Alternatively, you can attach a small but full rank D matrix to the original problem but remove the matrix of the reduced order model afterwards. As long as the size of D matrix is insignificant inside the control bandwidth, the reduced order model should be fairly close to the true model.

See Also
balmr, mrdemo, ohklmr, schmr

References
[1] U. B. Desai and D. Pal, "A Transformation Approach to Stochastic Model Reduction," IEEE Trans. on Automat. Contr., AC-29, 12, 1984.

[2] K. Glover, "Multiplicative Approximation of Linear Systems with L

Error Bounds," Proc. American Contr. Conf., Seattle, WA, June 18-20, 1986.

[3] E. A. Jonckheere and R. Li, "L

Error Bound for Phase Matching Approximation -- The One-Step-At-A-Time Hankel Norm Model Reduction," Int. J. Control, Vol. 46, no. 4, pp. 1343-1354, 1987.

[4] M. G. Safonov and R. Y. Chiang, "A Schur Method for Balanced Model Reduction," IEEE Trans. on Automat. Contr., vol. AC-34, no. 7, pp. 729-733, July 1989.

[5] M. G. Safonov and R. Y. Chiang, "Model Reduction for Robust Control: A Schur Relative-Error Method," Proc. American Contr. Conf., June 15-17, 1988.

[6] W. Wang and M. G. Safonov, "A Tighter Relative-Error Bound for Balanced Stochastic Truncation," Systems and Control Letters, 14, No. 4, pp. 307-317, 1990.

[7] W. Wang and M. G. Safonov, "A Relative Error Bound for Discrete Balanced Stochastic Truncation," Int. J. of Control, Vol. 54, No. 3, 1990.

[8] W. Wang and M. G. Safonov, "Comparison between Continuous and Discrete Balanced Stochastic Truncation Model Reduction," Proc. of Contr. and Decision Conf., Honolulu, Hawaii, 1990.

[9] W. Wang and M. G. Safonov, "Multiplicative-Error Bound for Balanced Stochastic Truncation Model Reduction," IEEE Trans. on Automat. Contr, vol. AC-37, no. 8, pp1265-1267, August 1992.

branch cgloci, dcgloci