Power System Blockset

Feedback Linearization Design

The input-output feedback linearization technique consists in the exact cancellation of the nonlinearities of the system in order to obtain a linear relationship between inputs and outputs in closed-loop. The nonlinear control law is deduced by successively differentiating each of the outputs until at least one input appears. Consider the first output as the terminal voltage V_t:

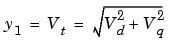
The terminal voltage is a complicated function of the state variables in which the control input V_fd appears explicitly with a multiplying factor of a very small order of magnitude. We therefore ignore this direct dependence between V_t and V_fd and compute the time derivate of output y₁:

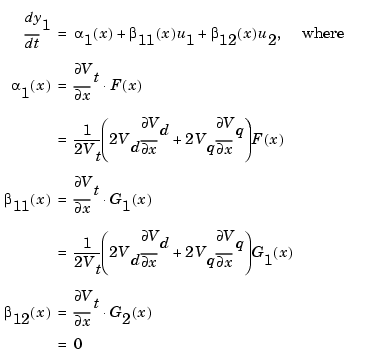
The second output y₂ is the angle 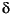that has to be differentiated three times before the inputs appear. This yields:

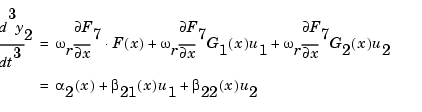
Combining the equations of the outputs, the following input-output nonlinear system is obtained

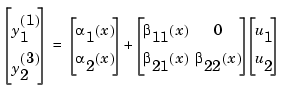
and the nonlinear control law is easily deduced.

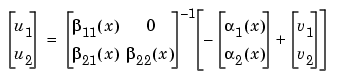
This will yield, in closed-loop, the exactly linearized input-output system

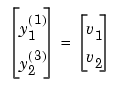
Once the system has been linearized, any linear control design can be applied to regulate the outputs. Here, the pole placement method was chosen and the following linear control law is proposed:

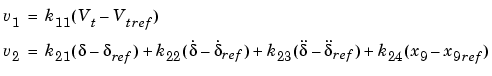
The last term in the equation of v₂ is introduced in order to stabilize the internal dynamics. These dynamics come about because the original nonlinear system is a ninth order while the linearized system is a fourth order. This is called partial linearization and we must ensure that the remaining dynamics are asymptotically stable. A complete treatment of this question can be found in reference [1].

Mathematical Model

Simulation Results