Power System Blockset

Units

In this manual, we use the International System of Units (SI).

Quantity	Unit	Symbol
Time	second	s
Length	meter	m
Mass	kilogram	kg
Energy	joule	J
Current	ampere	A
Voltage	volt	V
Active power	watt	W
Apparent power	volt ampere	VA
Reactive power	var	var
Impedance	ohm	,
Resistance	ohm	,
Inductance	henry	H
Capacitance	farad	F
Flux linkage	volt second	V. s
Rotation speed	radians per second revolutions per minute	rad/s rpm
Torque	newton meter	N.m
Inertia	kilogram (meter)2	kg.m2
Friction factor	newton meter second	N.m.s

We also use the per unit (p.u.) system on occasion to define the model parameters.

What Is the Per Unit System?

The per unit system is widely spread in the power system industry to express values of voltages, currents, powers and impedances of various power equipment. It is mainly used for transformers and AC machines.

For a given quantity (voltage, current, power, impedance, torque, etc.) the per unit value is the value related to a base quantity.

Generally the following two base values are chosen:

• The base power = nominal power of the equipment
• The base voltage = nominal voltage of the equipment

All other base quantities are derived from these two base quantities. Once the base power and the base voltage are chosen, the base current and the base impedance are determined by the natural laws of electrical circuits.

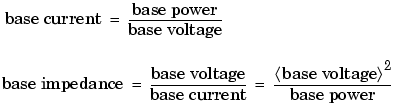
For a transformer with N windings, each having a different nominal voltage, the same base power is used for all windings (nominal power of the transformer). However, according to the above definitions, there are as many base values as windings for voltages, currents, and impedances.

For AC machines, the torque and speed can be also expressed in p.u. The following base quantities are chosen:

• The base speed = synchronous speed
• The base torque = torque corresponding at base power and synchronous speed:

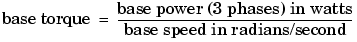
Instead of specifying the rotor inertia in kg*m², you would generally give the inertia constant H defined as:

The inertia constant is expressed in seconds. For large machines, this constant is around 3 to 5 seconds. An inertia constant of 3 seconds means that the energy stored in the rotating part could supply the nominal load during 3 seconds. For small machines, H is lower. For example, for a 3 HP motor, it can be between 0.5 and 0.7 seconds.

Example 1: Three-Phase Transformer

Let us consider, for example, a three-phase two winding transformer, The following typical parameters could be provided by the manufacturer:

• Nominal power = 300 kVA total for three phases
• Nominal frequency = 60 Hz
• Winding 1: connected in wye, nominal voltage = 25 kV rms line-to-line

resistance 0.01 p.u., leakage reactance = 0.02 p.u.

• Winding 2: connected in delta, nominal voltage = 600 V rms line-to-line

resistance 0.01 p.u., leakage reactance = 0.02 p.u.

• Magnetizing losses at nominal voltage in % of nominal current:

Resistive 1%, Inductive 1%

The base values for each single phase transformer are first calculated:

• For winding 1:

    base power : 300 kVA/3 = 100e3 VA/phase
    base voltage: 25 kV/sqrt(3) = 14434 V rms
    base current : 100e3/14434 = 6.928 A rms
    base impedance : 14434/6.928 = 2083
    base resistance : 14434/6.928 = 2083
    base inductance : 2083/(2pi*60)= 5.525 H

• For winding 2:

    base power : 300 kVA/3 = 100e3 VA
    base voltage: 600V rms
    base current : 100e3/600 = 166.7 A rms
    base impedance : 600/166.7 = 3.60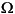
    base resistance : 600/166.7 = 3.60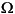
    base inductance : 3.60/(2pi*60) = 0.009549 H

The values of the winding resistances and leakage inductances expressed in SI units are therefore:

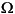• For winding 1: R1= 0.01* 2083 = 20.83 ; L1= 0.02*5.525 = 0.1105 H
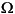• For winding 2: R2= 0.01* 3.60 = 0.0360 ; L2= 0.02*0.009549 = 0.191 mH

For the magnetizing branch, magnetizing losses of 1% resistive and 1% inductive mean a magnetizing resistance Rm of 100 p.u. and a magnetizing inductance Lm of 100 p.u. Therefore, the values expressed in SI units referred to winding 1 are:

Rm = 100*2083 = 208.3 k

Lm = 100*5.525 = 552.5 H

Example 2: Asynchronous Machine

Let us now consider the three-phase four-pole Asynchronous Machine in SI units provided in the Machines library of powerlib. It is rated 3 HP, 220 V rms line-to-line, 60 Hz.

The stator and rotor resistance and inductance referred to stator are:

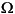• Rs= 0.435 ; Ls= 2 mH
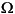• Rr=0.816 ; Lr=2 mH

The mutual inductance is Lm = 69.31mH. The rotor inertia is: J= 0.089 kg.m².

The base quantities for one phase are calculated as follows:

base power : 3 HP*746VA/3 = 746 VA/phase
    base voltage: 220 V/sqrt(3) = 127.0 V rms
    base current : 746/127.0 = 5.874 A rms
    base impedance : 127.0/5.874 = 21.62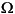
    base resistance : 127.0/5.874 = 21.62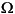
    base inductance : 21.62/(2pi*60)= 0.05735 H = 57.35 mH
    base speed : 1800 rpm = 1800*(2pi)/60 = 188.5 radians/second
    base torque (3phase):746*3/188.5 = 11.87 newton.meters

Using the above base values, you can compute the values in per units:

    Rs= 0.435 / 21.62 = 0.0201 p.u. Ls= 2 / 57.35 = 0.0349 p.u.
    Rr= 0.816 / 21.62 = 0.0377 p.u. Lr= 2 / 57.35 = 0.0349 p.u.
    Lm = 69.31/57.35 = 1.208 p.u.

The inertia is calculated from inertia J, synchronous speed, and nominal power:

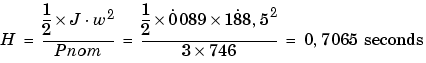
If you open the dialog box of the Asynchronous Machine block in p.u. units provided in the Machines library of powerlib, you will find that the parameters in p.u. are the ones calculated above.

Base Values for Instantaneous Voltage and Current Waveforms

When displaying instantaneous voltage and current waveforms on graphs or oscilloscopes, you normally consider the peak value of the nominal sinusoidal voltage as 1 p.u. In other words, the base values used for voltage and currents are the rms values given above multiplied by sqrt(2).

Why to Use the Per Unit System Instead of the Standard SI Units?

Here are main reasons for justifying the use of the per unit system:

1. When values are expressed in p.u., the comparison of electrical quantities with their "normal" value is straightforward.

For example, a transient voltage reaching a maximum of 1.42 p.u. indicates immediately that this voltage exceeds the nominal value by 42%.

2. The values of impedances expressed in p.u. stay fairly constant whatever the power and voltage ratings.

For example, for all transformers in the 3 kVA- 300 kVA power range, the leakage reactance varies approximately between 0.01 p.u. and 0.03 p.u., whereas the winding resistances vary between 0.01 p.u. and 0.005 p.u, whatever the nominal voltage. For transformers in the 300 kVA-300 MVA range, the leakage reactance varies approximately between 0.03 p.u. and 0.12 p.u, whereas the winding resistances vary between 0.005 p.u. and 0.002 p.u.

Similarly, for a salient pole synchronous machines, the synchronous reactance Xd is generally between 0.60 and 1.50 p.u whereas the sub transient reactance X'd is generally between 0.20 and 0.50 p.u.

It means that if you don't know the parameters for a 10 kVA transformer, you won't make a big mistake by assuming an average value of 0.02 p.u. for leakage reactances and 0.0075 p.u for winding resistances.

3. The calculations using the per unit system are simplified. When all impedances in a multivoltage power system are expressed on a common power base and on the nominal voltages of the different subnetworks, the total impedance in p.u. seen at one bus is obtained by simply adding all impedances in p.u, without taking into consideration the transformer ratios.

Using This Guide

About the Authors