Optimization Toolbox

Sequential Quadratic Programming (SQP)

SQP methods represent state-of-the-art in nonlinear programming methods. Schittowski [34], for example, has implemented and tested a version that out performs every other tested method in terms of efficiency, accuracy, and percentage of successful solutions, over a large number of test problems.

Based on the work of Biggs [1], Han [22], and Powell ([31],[32]), the method allows you to closely mimic Newton's method for constrained optimization just as is done for unconstrained optimization. At each major iteration an approximation is made of the Hessian of the Lagrangian function using a quasi-Newton updating method. This is then used to generate a QP subproblem whose solution is used to form a search direction for a line search procedure. An overview of SQP is found in Fletcher [13], Gill et al. [19], Powell [33], and Schittowski [23]. The general method, however, is stated here.

Given the problem description in GP (Eq. 2.1) the principal idea is the formulation of a QP subproblem based on a quadratic approximation of the Lagrangian function.

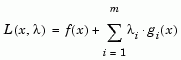
(2-25)

Here Eq. 2.1 is simplified by assuming that bound constraints have been expressed as inequality constraints. The QP subproblem is obtained by linearizing the nonlinear constraints.

Constrained Optimization

Quadratic Programming (QP) Subproblem