

| Mu Analysis and Synthesis Toolbox |   |
Compute upper and lower bounds for the complex and mixed (real and complex) structured singular value (referred to as mixed µ) of a VARYING/CONSTANT matrix
Syntax
[bnds,dvec,sens,pvec,gvec] = mu(matin,blk,options); [dl,dr,gl,gm,gr,pert] = muunwrap(dvec,gvec,pvec,blk); [dl,dr,gl,gm,gr] = muunwrap(dvec,gvec,blk); [dl,dr] = muunwrap(dvec,blk); pert = randel(blk,nrm,opt); [dl,dr] = unwrapd(dvec,blk); pert = unwrapp(pvec,blk);The functions associated with mixed µ are:
The default value of options is 'lu', meaning that a lower bound will be computed using the power method, Young and Doyle 1990 and Packard et al. 1988, and an upper bound will be computed, using the balanced/AMI technique, Young et al., 1992, for computing the upper bound from Fan et al., 1991.
Output arguments:[dl,dr,gl,gm,gr] =with respect to the values in Dl (and Dr). It is calculated in an ad-hoc manner, and is mainly used when fitting frequency varying Ds with rational functions via the routines inmuunwrap(dvec,gvec,blk); The upper bound inbndsfor a matrix M is a number> 0 such that there are scaling matrices Dl, Dr, Gl, Gm, Gr (
seeYoung et al., 1992, for details) satisfying
sensis a row vector which contains the sensitivity of
dkit, dkitgui, and autodkit.
pvec is a row vector containing a perturbation matrix that has the structure defined by blk. As with dvec and gvec, pvec is the same data type as matin and is stored as a vector. It can be unwrapped into the actual perturbation with the command, unwrapp:
pert = unwrapp(pvec,blk);
After being unwrapped, the perturbation matrix pert satisfies three conditions:
blk;
pert is equal to the reciprocal of the lower bound in bnds (when the lower bound is not zero);
mmult(matin,pert) has an eigenvalue equal to 1 at each independent variable.
Examples
Suppose sys is a system matrix with four inputs and four outputs, and that it is stable. sys_g is a frequency response of sys.
%  is 4 1 x 1 perturbation blocks
is 4 1 x 1 perturbation blocks
blk = ones(4,2);
% Calculate µ on frequency response
[bnds,dvec,sens,pvec] =mu(sys_g,blk);
% Unwrap the D scaling matrices
[dl,dr] =unwrapd(dvec,blk);
% Generate scaled matrix
dmdi =mmult(dl,sys_g,minv(dr));
% Verify the upper bound
vplot('liv,m',vnorm(dmdi),sel(bnds,1,1))
% Unwrap the perturbation
actpert =unwrapp(pvec,blk);
% Check that perturbation is correct structure
see(xtracti(actpert,1))
% Check lower bound and perturbation
vplot('liv,lm',sel(bnds,1,2),vnorm(actpert))
% Form M
mdel =mmult(sys_g,actpert);
% Verify M has an eigenvalue at 1
has an eigenvalue at 1
veig(mdel)
%  is 4 1 x 1 perturbation blocks
is 4 1 x 1 perturbation blocks
% with the first 2 real, and the last 2 complex
blk = [-1 0; -1 0; 1 0; 1 0];
% Calculate mixed µ on frequency response
[bnds,dvec,sens,pvec,gvec] =mu(sys_g,blk);
% Unwrap the D and G scaling matrices
[dl,dr,gl,gm,gr] =muunwrap(dvec,gvec,blk);
% Generate scaled matrix
dmd =mmult(dl,sys_g,minv(dr)); oobdmd =veval('*',dmd,minv(sel(bnds,1,1))); oobdmdjg =msub(oobdmd,mscl(gm,j)); scall =madd(eye(4),mmult(gl,gl)); scalr =madd(eye(4),mmult(gr,gr)); scall =veval(,scall,-0.25); scalr =veval(",scalr,-0.25); scaledmat =mmult(scall,oobdmdjg,scalr);
% Verify the upper bound (scaledmat should have norm 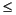 1)
1)
vplot('liv,m',vnorm(scaledmat))
% Unwrap the perturbation
pert=unwrapp(pvec,blk);
% Check that perturbation is correct structure
see(xtracti(pert,1))
% Check lower bound and perturbation
vplot('liv,m',sel(bnds,1,2),minv(vnorm(pert)))
% Form M
mdel =mmult(sys_g,pert);
% Verify M has an eigenvalue at 1
has an eigenvalue at 1
For more examples of computing bounds for µ, please refer to the "Computational Exercise with the mu Command" and "Computational Exercise with the mu Command -- Mixed Perturbations" sections in Chapter 4 as well as the robust multivariable control design examples in Chapters 6 and 7.see(veig(mdel))
Algorithm
Peter Young and Matt Newlin helped write the mu program and supporting routines.
Reference
S. Boyd, and L. El Ghaoui, "Methods of centers for minimizing generalized eigenvalues," Linear Algebra and Its Applications, vol. 188-189, pp. 63-111, 1993.
See Also
blknorm, dypert, genmu, norm, vnorm, vrho, vsvd
 | mscl, sclin, sclout | musynfit, musynflp, muftbtch |  |