

| Mu Analysis and Synthesis Toolbox |   |
dhfsyn computes an H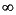 controller for a discrete-time SYSTEM interconnection matrix
controller for a discrete-time SYSTEM interconnection matrix
Syntax
[k,g,gfin,ax,ay,hamx,hamy] =dhfsyn(p,nmeas,ncon,...gmin,gmax,tol,h,z0,quiet,ricmethd,epr,epp)
Description
dhfsyn calculates a discrete-time H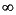 controller that achieves the infinity norm
controller that achieves the infinity norm gfin for the interconnection structure p. The controller, k, stablizes the discrete-time SYSTEM matrix p and has the same number of states as p. The SYSTEM p is partitioned
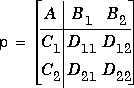
ncon) and C2 has row size (nmeas).
The closed-loop system is returned in g. The same bilinear transformation method described for dhfnorm is used. The controller k is returned that minimizes the entropy integral,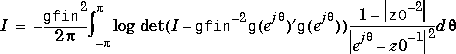
hinfsyne and the corresponding conditions and tests need to be satisfied.
Input argumentsax, ay, hamx, and hamy correspond to the equivalent continuous-time problems and can also be scaled and/or balanced.
The dhfsyn program outputs several variables, which can be checked to ensure that the above conditions are being met. For each 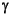 value the minimum magnitude, real part of the eigenvalues of the X Hamiltonian matrices is displayed along with the minimum eigenvalue of X
value the minimum magnitude, real part of the eigenvalues of the X Hamiltonian matrices is displayed along with the minimum eigenvalue of X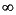 , which is the solution to the X Riccati equation. A # sign is placed to the right of the condition that failed in the printout. This additional information can aid you in the control design process.
, which is the solution to the X Riccati equation. A # sign is placed to the right of the condition that failed in the printout. This additional information can aid you in the control design process.
Algorithm
dhfsyn uses the above bilinear transformation to continuous-time and then the formulae described in the Glover and Doyle paper for solution to the optimal H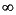 control design problem.
control design problem.
hinfsyne, hinf_st, hinf_gam, hinfe_c:
hinf_gam calls ric_eig, ric_schr, csord, and cgivens
Reference
Doyle, J.C., K. Glover, P. Khargonekar, and B. Francis, "State-space solutions to standard H2 and H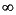 control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.
control problems," IEEE Transactions on Automatic Control, vol. 34, no. 8, pp. 831-847, August 1989.
norm bound and relations to risk sensitivity," Systems and Control Letters, vol. 11, pp. 167-172, 1988.
See Also
hinfsyne, hinffi, hinfnorm, hinfsyn, h2syn, h2norm, ric_eig, ric_schr, sdhfnorm, sdhfsyn
 | dhfnorm | dkit |  |