Mapping Toolbox

areaquad

Compute area of a latitude-longitude quadrangle

Syntax

area = areaquad(lat1,lon1,lat2,lon2)
area = areaquad(lat1,lon1,lat2,lon2,geoid)
area = areaquad(lat1,lon1,lat2,lon2,units)
area = areaquad(lat1,lon1,lat2,lon2,geoid,units)

Description

A latitude-longitude quadrangle is a region bounded by two meridians and two parallels. In spherical geometry, it is the intersection of a lune (a section bounded by two meridians) and a zone (a section bounded by two parallels).

area = areaquad(lat1,lon1,lat2,lon2) returns the surface area bounded by the parallels lat1 and lat2 and the meridians lon1 and lon2. The output area is a fraction of the unit sphere's area of 4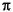, so the result ranges from 0 to 1.

area = areaquad(lat1,lon1,lat2,lon2,geoid) allows the specification of the geoid model with the two-element geoid vector geoid. When a geoid is input, the resulting area is given in terms of the (squared) units of the geoid. For example, if the geoid almanac('earth','geoid','kilometers') is used, the resulting area will be in km². The default geoid is the unit sphere.

area = areaquad(lat1,lon1,lat2,lon2,geoid,units) specifies the units of the inputs, which are 'degrees' by default.

Examples

What fraction of the Earth's surface lies between 30ºN and 45ºN, and also between 25ºW and 60ºE?

area = areaquad(30,-25,45,60)
area =
    0.0245

About 2.5%. What is the surface area of the Earth in square kilometers if a spherical geoid is assumed (use the almanac function with the sphere as its reference body)?

earthgeoid = almanac('earth','geoid','km','sphere');
area = areaquad(-90,-180,90,180,earthgeoid)
area =
   5.1006e+08

For comparison:

almanac('earth','surfarea','km')
ans =
   5.1006e+08

Remarks

This calculation is exact, being based on simple spherical geometry. For nonspherical geoids, the data is converted to the auxiliary authalic sphere.

See Also

almanac	Planetary data
areaint areamat	Other area calculations

areamat

aut2geod