Image Processing Toolbox

Transforms

Overview

The usual mathematical representation of an image is a function of two spatial variables: 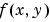. The value of the function at a particular location 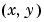represents the intensity of the image at that point. The term transform refers to an alternative mathematical representation of an image.

For example, the Fourier transform is a representation of an image as a sum of complex exponentials of varying magnitudes, frequencies, and phases. This representation is useful in a broad range of applications, including (but not limited to) image analysis, restoration, and filtering.

The discrete cosine transform (DCT) also represents an image as a sum of sinusoids of varying magnitudes and frequencies. The DCT is extremely useful for image compression; it is the basis of the widely used JPEG image compression algorithm.

The Radon transform represents an image as a collection of projections along various directions. It is used in areas ranging from seismology to computer vision.

This chapter defines each of these transforms, describes related toolbox functions, and shows examples of related image processing applications.

Words You Need to Know

An understanding of the following terms will help you to use this chapter. For more explanation of this table and others like it, see Words You Need to Know in the Preface. Note that this table includes brief definitions of terms related to transforms; a detailed discussion of these terms and the theory behind transforms is outside the scope of this User's Guide.

Words
Definitions

Discrete transform
A transform whose input and output values are discrete samples, making it convenient for computer manipulation. Discrete transforms implemented by MATLAB and the Image Processing Toolbox include the discrete Fourier transform (DFT) and the discrete cosine transform (DCT).

Frequency domain
The domain in which an image is represented by a sum of periodic signals with varying frequency.

Inverse transform
An operation that when performed on a transformed image, produces the original image.

Spatial domain
The domain in which an image is represented by intensities at given points in space. This is the most common representation for image data.

Transform
An alternative mathematical representation of an image. For example, the Fourier transform is a representation of an image as a sum of complex exponentials of varying magnitudes, frequencies, and phases. Transforms are useful for a wide range of purposes, including convolution, enhancement, feature detection, and compression.

Words	Definitions
Discrete transform	A transform whose input and output values are discrete samples, making it convenient for computer manipulation. Discrete transforms implemented by MATLAB and the Image Processing Toolbox include the discrete Fourier transform (DFT) and the discrete cosine transform (DCT).
Frequency domain	The domain in which an image is represented by a sum of periodic signals with varying frequency.
Inverse transform	An operation that when performed on a transformed image, produces the original image.
Spatial domain	The domain in which an image is represented by intensities at given points in space. This is the most common representation for image data.
Transform	An alternative mathematical representation of an image. For example, the Fourier transform is a representation of an image as a sum of complex exponentials of varying magnitudes, frequencies, and phases. Transforms are useful for a wide range of purposes, including convolution, enhancement, feature detection, and compression.

Computing the Frequency Response of a Filter Fourier Transform