System Identification

ivar

Estimate the parameters of an AR model using an approximately optimal choice of instrumental variable procedure.

Syntax

m = ivar(y,na)
m = ivar(y,na,nc,maxsize)

Description

The parameters of an AR model structure

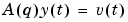
are estimated using the instrumental variable method. y is the signal to be modeled, entered as an iddata object (outputs only). na is the order of the A polynomial (the number of A parameters). The resulting estimate is returned as an idpoly model m. The routine is for scalar signals only.

In the above model, 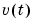is an arbitrary process, assumed to be a moving average process of order nc, possibly time varying. (Default is nc = na.) Instruments are chosen as appropriately filtered outputs, delayed nc steps.

The optional argument maxsize is explained under Algorithm Properties.

Examples

Compare spectra for sinusoids in noise, estimated by the IV method and estimated by the forward-backward least-squares method.

y = iddata(sin([1:500]'*1.2) + sin([1:500]'*1.5) + 
0.2*randn(500,1),[]);
miv = ivar(y,4);
mls = ar(y,4);
bode(miv,mls)

See Also

ar, etfe, spa

References

Stoica, P. et al., Optimal Instrumental variable estimates of the AR-parameters of an ARMA process, IEEE Trans. Autom. Control, Vol AC-30, 1985, pp. 1066-1074.

init

ivstruc