

| Fuzzy Logic Toolbox |   |
Sugeno-Type Fuzzy Inference
The fuzzy inference process we've been referring to so far is known as Mamdani's fuzzy inference method. It's the most commonly seen fuzzy methodology. In this section we discuss the so-called Sugeno, or Takagi-Sugeno-Kang method of fuzzy inference first introduced in 1985 [Sug85]. It is similar to the Mamdani method in many respects. In fact the first two parts of the fuzzy inference process, fuzzifying the inputs and applying the fuzzy operator, are exactly the same. The main difference between Mamdani-type of fuzzy inference and Sugeno-type is that the output membership functions are only linear or constant for Sugeno-type fuzzy inference.
A typical fuzzy rule in a zero-order Sugeno fuzzy model has the form
where A and B are fuzzy sets in the antecedent, while k is a crisply defined constant in the consequent. When the output of each rule is a constant like this, the similarity with Mamdani's method is striking. The only distinctions are the fact that all output membership functions are singleton spikes, and the implication and aggregation methods are fixed and can not be edited. The implication method is simply multiplication, and the aggregation operator just includes all of the singletons.
The figure above shows the fuzzy tipping model developed in previous sections of this manual adapted for use as a zero-order Sugeno system. Fortunately it is frequently the case that singleton output functions are completely sufficient for a given problem's needs. As an example, the system tippersg.fis is the Sugeno-type representation of the now-familiar tipping model. If you load the system and plot its output surface, you will see it is almost the same as the Mamdani system we've been looking at.
a = readfis('tippersg');
gensurf(a)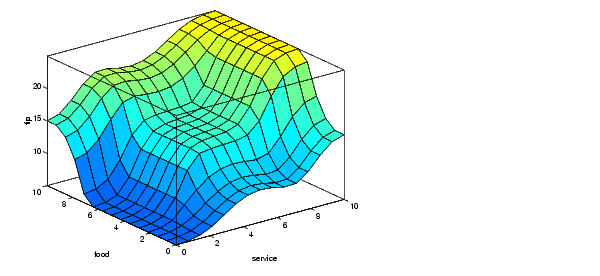
The more general first-order Sugeno fuzzy model has rules of the form
where A and B are fuzzy sets in the antecedent, while p, q, and r are all constants. The easiest way to visualize the first-order system is to think of each rule as defining the location of a "moving singleton." That is, the singleton output spikes can move around in a linear fashion in the output space, depending on what the input is. This also tends to make the system notation very compact and efficient. Higher order Sugeno fuzzy models are possible, but they introduce significant complexity with little obvious merit. Sugeno fuzzy models whose output membership functions are greater than first order are not supported by the Fuzzy Logic Toolbox.
Because of the linear dependence of each rule on the system's input variables, the Sugeno method is ideal for acting as an interpolating supervisor of multiple linear controllers that are to be applied, respectively, to different operating conditions of a dynamic nonlinear system. For example, the performance of an aircraft may change dramatically with altitude and Mach number. Linear controllers, though easy to compute and well-suited to any given flight condition, must be updated regularly and smoothly to keep up with the changing state of the flight vehicle. A Sugeno fuzzy inference system is extremely well suited to the task of smoothly interpolating the linear gains that would be applied across the input space; it's a natural and efficient gain scheduler. Similarly, a Sugeno system is suited for modeling nonlinear systems by interpolating multiple linear models.
 | Building Your Own Fuzzy Simulink Models | An Example: Two Lines |  |