

| Fixed-Point Blockset |   |
The FixPt Integrator: Forward realization is a masked subsystem that performs discrete-time integration using the Forward Euler method. The Forward Euler method is also known as the Forward Rectangular method or left-hand approximation. For this method, integration is approximated by the z-domain transfer function
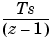
where Ts is the sampling period. The realization is shown below.
As shown in the figure, the transfer function yields the difference equation
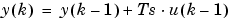
where k is the current time step, k - 1 is the previous time step, y(k) is the current output, y(k - 1) is the output from the previous time step, and u(k - 1) is the input from the previous time step.
Parameters and Dialog Box
The parameters and dialog box for the forward integrator realization are the same as those for the trapezoidal integrator realization, and are given in Parameters and Dialog Box.
Model Design Review
The model design issues are the same as those for the trapezoidal integrator as described in Model Design Review.
 | Backward Integration | Derivative Realizations |  |