Fixed-Point Blockset

Shifts

Nearly all microprocessors and digital signal processors support well-defined bit-shift (or simply shift) operations for integers. For example, consider the 8-bit unsigned integer 00110101. The results of a 2-bit shift to the left and a 2-bit shift to the right are shown below.

Shift Operation	Binary Value	Decimal Value
No shift (original number)	00110101	53
Shift left by 2 bits	11010100	212
Shift right by 2 bits	00001101	13

You can perform a shift with the Fixed-Point Blockset using either the FixPt Conversion block or the FixPt Gain block. The FixPt Conversion block shifts both the bits and radix point while the FixPt Gain block shifts the bits but not the radix point. These two modes of shifting as well as shifting to the right are discussed below.

Note    Performing a "plain" or "raw" machine-level shift such as those given in the example above with the Fixed-Point Blockset is complicated by the available scaling options. Therefore, a single "FixPt Shift" block is not provided. For more information about scaling, refer to Scaling.

Shifting to the Right

Shifts to the right can be classified as a logical shift right or an arithmetic shift right. For a logical shift right, a 0 is incorporated into the most significant bit for each bit shift. For an arithmetic shift right, the most significant bit is recycled for each bit shift. With the Fixed-Point Blockset, shifting to the right follows these rules:

• For signed numbers, an arithmetic shift right is performed. Therefore, the most significant bit is recycled for each bit shift. For example, given the signed fixed-point number 10110.101, a bit shift two places to the right with the radix point unmoved yields the number 11101.101.
• For unsigned numbers, a logical shift right is performed. Therefore, the most significant bit is a 0 for each bit shift. For example, given the unsigned fixed-point number 10110.101, a bit shift two places to the right with the radix point unmoved yields the number 00101.101.

Shifting Bits and the Radix Point

With the FixPt Conversion block, you can perform a shift operation on the input by specifying the appropriate radix point-only scaling for the output. This block shifts both the bits and the radix point.

In most cases, you will perform a "plain" or "raw" shift. To perform such a shift using the FixPt Conversion block, you must configure the block's dialog box this way:

• The output data type is identical to the input data type.
• The rounding mode is set to Floor. Therefore, bits simply fall off the left or fall off the right when a shift occurs.
• Overflows wrap.
• The output scaling is specified to reflect the required shift.

For example, suppose you start with the fixed-point number 00110.101 (a decimal value of 6.625), which is characterized by the blockset as an 8-bit unsigned, generalized fixed-point number with radix point-only scaling of 2^-3. To shift the bits and radix point two places to the right, the input scaling of 2^-3 is multiplied by 2², which yields a scaling of 2^-1. To shift the bits and radix point two places to the left, the input scaling of 2^-3 is multiplied by 2^-2, which yields as scaling of 2^-5. This situation is shown below

Shift Operation	Scaling	Binary Value	Decimal Value
No shift (original number)	2-3	00110.101	6.625
Shift right by 2 bits	2-1	0000110.1	6.5
Shift left by 2 bits	2-5	110.10100	6.625

.

The figure below shows the fixed-point model used to generate the above data.

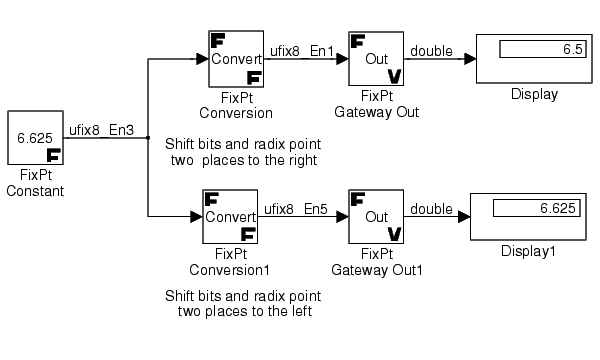
Refer to Chapter 9, Block Reference for more information about the FixPt Conversion block.

Shifting Bits but Not the Radix Point

With the FixPt Gain block, you can perform a shift operation on the input by specifying the gain as a power of two. This block shifts only the bits and not the radix point.

In most cases, you will perform a plain or raw shift. To perform such a shift using the FixPt Gain block, you must configure the block's dialog box this way:

• The output data type is identical to the input data type.
• The rounding mode is set to Floor. Therefore, bits simply fall off the left or fall off the right when a shift occurs.
• Overflows wrap.
• The gain is specified as the appropriate power of 2 to reflect the required shift.

For example, suppose you start with the same fixed-point number, 00110.101, defined above. To shift the bits two places to the left, a gain of 4 is specified, and to shift the bits two places to the right, a gain of 0.25 is specified. This situation is shown below

Shift Operation	Gain Value	Binary Value	Decimal Value
N/A (original number)	2-3	00110.101	6.625
Shift left by 2 bits	4	11010.100	26.5
Shift right by 2 bits	0.25	00001.101	1.625

.

The figure below shows the fixed-point model used to generate the above data.

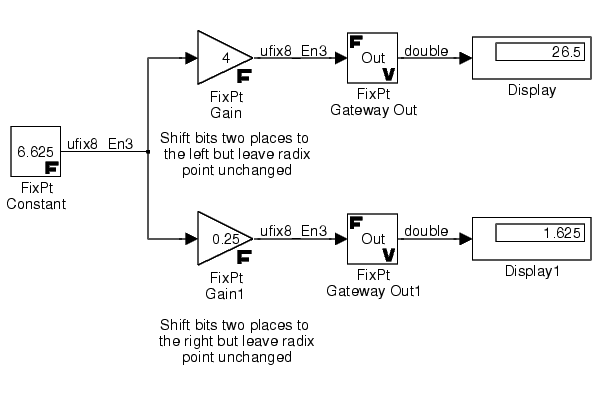
Refer to Chapter 9, Block Reference for more information about the FixPt Gain block.

Division

Example: Conversions and Arithmetic Operations