

| DSP Blockset |   |
Factor a matrix using singular value decomposition.
Library
Math Functions / Matrices and Linear Algebra / Matrix Factorizations
Description
The Singular Value Decomposition block factors the M-by-N input matrix A such that
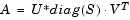
where U is an M-by-P matrix, V is an N-by-P matrix, S is a length-P vector, and P is defined as min(M,N).
When M = N, U and V are both M-by-M unitary matrices. When M > N, V is an N-by-N unitary matrix, and U is an M-by-N matrix whose columns are the first N columns of a unitary matrix. When N > M, U is an M-by-M unitary matrix, and V is an M-by-N matrix whose columns are the first N columns of a unitary matrix. In all cases, S is a 1-D vector of positive singular values having length P. The output is always sample-based.
Length-N row inputs are treated as length-N columns.
[U,S,V] = svd(A,0) % Equivalent MATLAB code for M > N
Note that the first (maximum) element of output S is equal to the 2-norm of the matrix A.
You can enable the U and V output ports by selecting the Output the singular vectors parameter.
Dialog Box
U and V output ports when selected.References
Golub, G. H., and C. F. Van Loan. Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.
See Also
| Autocorrelation LPC |
DSP Blockset |
| Cholesky Factorization |
DSP Blockset |
| LDL Factorization |
DSP Blockset |
| LU Inverse |
DSP Blockset |
| Pseudoinverse |
DSP Blockset |
| QR Factorization |
DSP Blockset |
| SVD Solver |
DSP Blockset |
svd |
MATLAB |
See Factoring Matrices for related information.
 | Sine Wave | Sort |  |